如何设计拱桥景观灯的悬挂方案? | |||
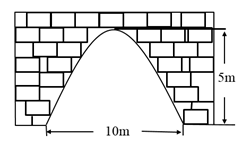
素材1 | 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 20m ,拱顶离水面 5m .据调查,该河段水位在此基础上再涨 1.8m 达到最高. |
| |
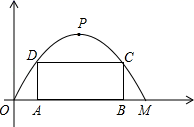
素材2 | 为迎佳节,拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼,如图3.为了安全,灯笼底部距离水面不小于 1m ;为了实效,相邻两盏灯笼悬挂点的水平间距均为 1.6m ;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布. |
| |
问题解决 | |||
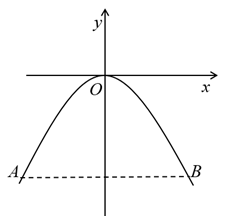
任务1 | 确定桥拱形状 | 在图2中建立合适的直角坐标系,求抛物线的函数表达式. | |
任务2 | 探究悬挂范围 | 在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围. | |
任务3 | 拟定设计方案 | 给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标. | |

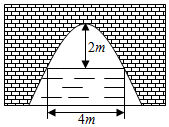

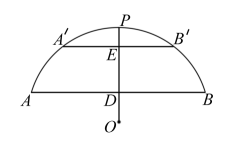

①求抛物线的解析式;②要使高为3米的船通过,则其宽度须不超过多少米?

①求圆的半径;②要使高为3米的船通过,则其宽度须不超过多少米?

通过取点、测量,数学小组的同学得到了x与y的几组值,如下表:
x(米) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y(米) | 0 | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | 1.75 | 0 |


x(米) | 0 | 2 | 4 | 6 | 8 |
y(米) | 4.0 | 5.5 | 6.0 | 5.5 | 4.0 |




探究一:

①求左、右面两条钢缆的最低点之间的距离是多少?
②求安全绳长度(钢缆和桥面之间距离)的最小值是多少?
请解决以下问题:

|
x(米) |
0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
|
y(米) |
3.00 |
3.44 |
3.76 |
3.94 |
3.99 |
3.92 |
3.78 |
3.42 |
3.00 |

