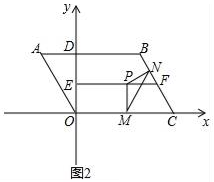
①若G为BD上任意一点,则AG=EF;
②若BG=AB,则∠DAG=22.5°;
③若G为BD的中点,则四边形CEGF是正方形;
④若DG:BG=1:3,则S△ADG=
则其中正确的是.
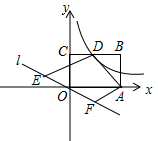

①如图3,若 ,
, 则
;
②如图4,连接 , 将
沿着
翻折,点
落在点
处,
的中点为
, 则
的最小值为.

∵ ,
∴ ,
∴ ,
只有当
时,
.
结论:在均为正实数
中,若
为定值
, 则
只有当
时,
有最小值
, 根据上述内容,回答下列问题:
问题:若
, 当
时,
有最小值为.
问题:若函数
, 则当
时,函数
有最小值为.






小明同学探究此问题的方法是:过P点作于E点,
于F点,根据正方形的性质和角平分线的性质,得出
, 再证明
, 可得出结论,他的结论应是 ;并证明该结论.
数学课上老师出示了这样一个问题:如图1,等腰Rt△PBF的直角顶点P在正方形ABCD的边AD上,斜边BF交CD于点Q,连接PQ.请探索PQ、AP、CQ的数量关系.
某学习小组的同学经过探索,交流了自己的想法:利用现在所学的旋转知识,可将△ABP旋转到△CBE位置,然后通过证明△BPQ≌△BEQ来探索数量关系.
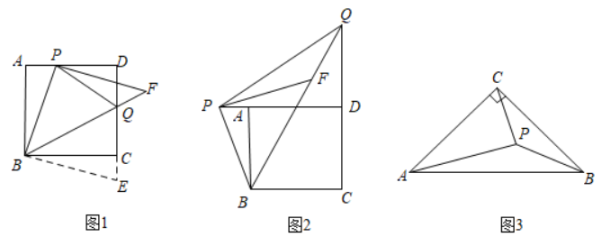





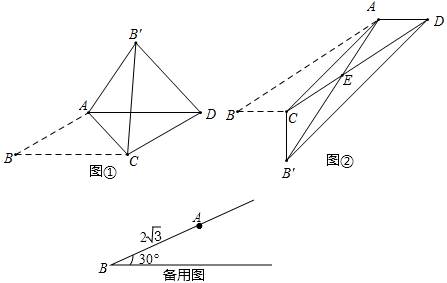
在▱ABCD中, ,将
沿AC翻折至
,连接
.
结论1: //AC;
结论2: 与▱ABCD重叠部分的图形是等腰三角形.
请利用图①证明结论1或结论2(只需证明一个结论).
在▱ABCD中,已知∠B=30°,将 沿AC翻折至
,连接
.



①若t=1,当旋转角为30°、、、、210°、时这支铅笔与线段AB、AC共围成6个等腰三角形;
②当这支铅笔与线段AB、AC正好围成5个等腰三角形时,求t的取值范围;
③当这支铅笔与线段AB、AC正好围成3个等腰三角形时,直接写出t的取值范围.