
 B .
B .  C .
C .  D .
D . 
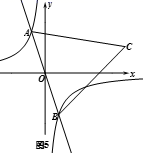

①点 、
横坐标之和是否为定值,若是定值,请求出;若不是,请说明理由.
②当 时,平行四边形
能否为菱形;若能,求出菱形的周长:若不能,请说明理由.
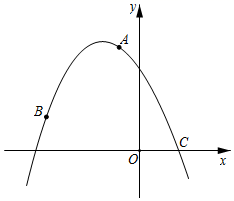
①求点A、B、C的坐标;
②如果点P是抛物线上一点,点M是该抛物线对称轴上的点,当 是以
为斜边的等腰直角三角形时,求出点P的坐标;
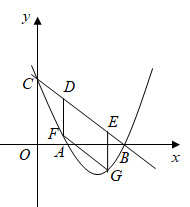
①若 将
的面积分为1:2两部分,求点P的坐标;
②当 时,直线
上是否存在一点Q,使
?如果存在,求出点Q的坐标;如果不存在,请说明理由
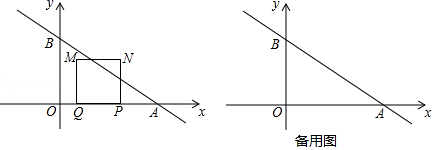

①求点 的坐标;
②点 是直线
上一点,若对于在第一象限内的抛物线
上的动点
始终有
,请直接写出
的取值范围.
