备考2023年中考数学压轴题训练 ——二次函数（1）

更新时间：2023-05-14 浏览次数：215 类型：三轮冲刺

一、真题

1. (2022·台州) 如图1，灌溉车沿着平行于绿化带底部边线l的方向行驶，为绿化带浇水．喷水口H离地竖直高度为h（单位： m）．如图2，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象；把绿化带横截面抽象为矩形 DEFG ，其水平宽度DE=3m，竖直高度为EF的长．下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2m，高出喷水口0.5m，灌溉车到l 的距离OD为d（单位：m）．
1. （1）若h=1.5，EF=0.5m；
  ①求上边缘抛物线的函数解析式，并求喷出水的最大射程 OC；
  
  ②求下边缘抛物线与x 轴的正半轴交点B的坐标；
  
  ③要使灌溉车行驶时喷出的水能浇灌到整个绿化带，求d的取值范围；
2. （2）若 EF=1m．要使灌溉车行驶时喷出的水能浇灌到整个绿化带，请直接写出h的最小值．
答案解析收藏纠错 + 选题
2. (2022·宿迁) 如图，二次函数 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ (0，0)， $\text{[math]}$ (4，0)两点，顶点为 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，若点 $\text{[math]}$ 是线段 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠后，点 $\text{[math]}$ 落在点 $\text{[math]}$ 的位置，线段 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，且点 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 点不重合.
1. （1）求二次函数的表达式；
2. （2） ①求证： $\text{[math]}$ ；
  ②求 $\text{[math]}$ ；
3. （3）当 $\text{[math]}$ 时，求直线 $\text{[math]}$ 与二次函数的交点横坐标.
答案解析收藏纠错 + 选题
3. (2022·盐城) 【发现问题】
小明在练习簿的横线上取点 $\text{[math]}$ 为圆心，相邻横线的间距为半径画圆，然后半径依次增加一个间距画同心圆，描出了同心圆与横线的一些交点，如图1所示，他发现这些点的位置有一定的规律．
【提出问题】
小明通过观察，提出猜想：按此步骤继续画圆描点，所描的点都在某二次函数图象上．
1. （1）【分析问题】
  小明利用已学知识和经验，以圆心 $\text{[math]}$ 为原点，过点 $\text{[math]}$ 的横线所在直线为 $\text{[math]}$ 轴，过点 $\text{[math]}$ 且垂直于横线的直线为 $\text{[math]}$ 轴，相邻横线的间距为一个单位长度，建立平面直角坐标系，如图2所示．当所描的点在半径为5的同心圆上时，其坐标为．
2. （2）【解决问题】
  请帮助小明验证他的猜想是否成立．
3. （3）【深度思考】
  小明继续思考：设点 $\text{[math]}$ ， $\text{[math]}$ 为正整数，以 $\text{[math]}$ 为直径画 $\text{[math]}$ ，是否存在所描的点在 $\text{[math]}$ 上．若存在，求 $\text{[math]}$ 的值；若不存在，说明理由．
答案解析收藏纠错 + 选题
4. (2022·南通) 定义：函数图象上到两坐标轴的距离都不大于 $\text{[math]}$ 的点叫做这个函数图象的“n阶方点”．例如，点 $\text{[math]}$ 是函数 $\text{[math]}$ 图像的“ $\text{[math]}$ 阶方点”；点 $\text{[math]}$ 是函数 $\text{[math]}$ 图像的“2阶方点”．
1. （1）在① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ 三点中，是反比例函数 $\text{[math]}$ 图像的“1阶方点”的有（填序号）；
2. （2）若y关于x的一次函数 $\text{[math]}$ 图像的“2阶方点”有且只有一个，求a的值；
3. （3）若y关于x的二次函数 $\text{[math]}$ 图像的“n阶方点”一定存在，请直接写出n的取值范围．
答案解析收藏纠错 + 选题
5. (2022·徐州) 如图，在△ABC中，∠BAC＝90°，AB＝AC＝12，点P在边AB上，D、E分别为BC、PC的中点，连接DE．过点E作BC的垂线，与BC、AC分别交于F、G两点．连接DG，交PC于点H．
1. （1） ∠EDC的度数为；
2. （2）连接PG，求△APG 的面积的最大值；
3. （3） PE与DG存在怎样的位置关系与数量关系？请说明理由；
4. （4）求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题
6. (2022·安徽) 如图1，隧道截面由抛物线的一部分AED和矩形ABCD构成，矩形的一边BC为12米，另一边AB为2米．以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系xOy，规定一个单位长度代表1米．E（0，8）是抛物线的顶点．
1. （1）求此抛物线对应的函数表达式；
2. （2）在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点 $\text{[math]}$ ， $\text{[math]}$ 在x轴上，MN与矩形 $\text{[math]}$ 的一边平行且相等．栅栏总长l为图中粗线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， MN长度之和．请解决以下问题：
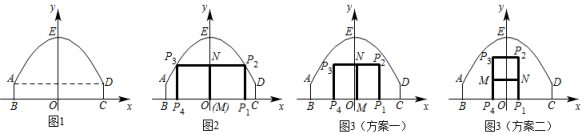
  （ⅰ）修建一个“”型栅栏，如图2，点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线AED上．设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，求栅栏总长l与m之间的函数表达式和l的最大值；
  （ⅱ）现修建一个总长为18的栅栏，有如图3所示的修建“”型或“”型栅型两种设计方案，请你从中选择一种，求出该方案下矩形 $\text{[math]}$ 面积的最大值，及取最大值时点 $\text{[math]}$ 的横坐标的取值范围（ $\text{[math]}$ 在 $\text{[math]}$ 右侧）．
答案解析收藏纠错 + 选题
7. (2022·福建) 在平面直角坐标系xOy中，已知抛物线 $\text{[math]}$ 经过A（4，0），B（1，4）两点.P是抛物线上一点，且在直线AB的上方.
1. （1）求抛物线的解析式；
2. （2）若△OAB面积是△PAB面积的2倍，求点P的坐标；
3. （3）如图，OP交AB于点C， $\text{[math]}$ 交AB于点D.记△CDP，△CPB，△CBO的面积分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .判断 $\text{[math]}$ 是否存在最大值.若存在，求出最大值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
8. (2022·齐齐哈尔) 综合与探究
如图，某一次函数与二次函数 $\text{[math]}$ 的图象交点为A（-1，0），B（4，5）．
1. （1）求抛物线的解析式；
2. （2）点C为抛物线对称轴上一动点，当AC与BC的和最小时，点C的坐标为；
3. （3）点D为抛物线位于线段AB下方图象上一动点，过点D作DE⊥x轴，交线段AB于点E，求线段DE长度的最大值；
4. （4）在（2）条件下，点M为y轴上一点，点F为直线AB上一点，点N为平面直角坐标系内一点，若以点C，M，F，N为顶点的四边形是正方形，请直接写出点N的坐标．
答案解析收藏纠错 + 选题
9. (2022·大庆) 已知二次函数 $\text{[math]}$ 图象的对称轴为直线 $\text{[math]}$ ．将二次函数 $\text{[math]}$ 图象中y轴左侧部分沿x轴翻折，保留其他部分得到新的图象C．
1. （1）求b的值；
2. （2） ①当 $\text{[math]}$ 时，图象C与x轴交于点M，N（M在N的左侧），与y轴交于点P．当 $\text{[math]}$ 为直角三角形时，求m的值；
  ②在①的条件下，当图象C中 $\text{[math]}$ 时，结合图象求x的取值范围；
3. （3）已知两点 $\text{[math]}$ ，当线段 $\text{[math]}$ 与图象C恰有两个公共点时，直接写出m的取值范围．
答案解析收藏纠错 + 选题
10. (2022·哈尔滨) 在平面直角坐标系中，点O为坐标原点，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，点 $\text{[math]}$ ，与y轴交于点C．
1. （1）求a，b的值；
2. （2）如图1，点D在该抛物线上，点D的横坐标为 $\text{[math]}$ ，过点D向y轴作垂线，垂足为点E．点P为y轴负半轴上的一个动点，连接 $\text{[math]}$ 、设点P的纵坐标为t， $\text{[math]}$ 的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
3. （3）如图2，在（2）的条件下，连接 $\text{[math]}$ ，点F在 $\text{[math]}$ 上，过点F向y轴作垂线，垂足为点H，连接 $\text{[math]}$ 交y轴于点G，点G为 $\text{[math]}$ 的中点，过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N，连接 $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点M，点R在 $\text{[math]}$ 上，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求直线 $\text{[math]}$ 的解析式．
答案解析收藏纠错 + 选题

二、综合题

11. (2023·亳州模拟) 如图1，灌溉车沿着平行于绿化带底部边线的方向行驶，为绿化带浇水．喷水口H离地竖直高度为hm，如图2，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象，把绿化带横截面抽象为矩形 $\text{[math]}$ ．下边缘抛物线是由上边缘抛物线向左平移得到的，上边缘抛物线最高点A离喷水口的水平距离为2m，高出喷水口0.5m，灌溉车到绿化带的距离 $\text{[math]}$ 为d m．当 $\text{[math]}$ m， $\text{[math]}$ m， $\text{[math]}$ m时，解答下列问题：
1. （1） ①求上边缘抛物线的函数解析式，并求喷出水的最大射程 $\text{[math]}$ ；
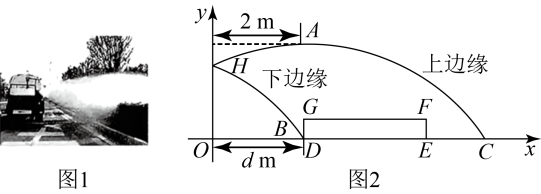
  ②求出点B的坐标；
2. （2）要使灌溉车行驶时喷出的水能浇灌到整个绿化带，试求出d的取值范围．
答案解析收藏纠错 + 选题
12. (2023·滁州模拟) 抛物线 $\text{[math]}$ 与坐标轴的正半轴分别交于A，B两点，其中 $\text{[math]}$ ．
1. （1）如图1，求抛物线 $\text{[math]}$ 的表达式，并求点B的横坐标；
2. （2）如图2，将抛物线 $\text{[math]}$ 向左平移，使得平移后的抛物线 $\text{[math]}$ 经过点A，且点B的对应点为C，求 $\text{[math]}$ 的长；
3. （3）如图3，矩形 $\text{[math]}$ 的顶点D，G都在x轴上， $\text{[math]}$ ，且 $\text{[math]}$ ，把两条抛物线 $\text{[math]}$ ， $\text{[math]}$ 及线段 $\text{[math]}$ 围成的封闭图形的内部记为区域M，要使矩形 $\text{[math]}$ 在区域M的内部（包括边界），求d的取值范围．
答案解析收藏纠错 + 选题
13. (2023九下·南平模拟) 如图1，抛物线 $\text{[math]}$ 与x轴相交于原点O和点A，直线 $\text{[math]}$ 与抛物线在第一象限的交点为B点，抛物线的顶点为C点.
1. （1）求点B和点C的坐标；
2. （2）抛物线上是否存在点D，使得 $\text{[math]}$ ？若存在，求出所有点D的坐标；若不存在，请说明理由；
3. （3）如图2，点E是点B关于抛物线对称轴的对称点，点F是直线 $\text{[math]}$ 下方的抛物线上的动点， $\text{[math]}$ 与直线 $\text{[math]}$ 交于点G.设 $\text{[math]}$ 和 $\text{[math]}$ 的面积分别为 $\text{[math]}$ 和 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
14. (2023·金华模拟) 如图1，在平面直角坐标系中，四边形AOBC为矩形，BC= $\text{[math]}$ ， ∠BOC=60°，D为BC中点.某反比例函数过点D，且与直线OC交于点E.
1. （1）点E的坐标为.
2. （2）好奇的小明在探索一个新函数.若点P为x轴上一点，过点P作x轴的垂线交直线AC于点Q，交该反比例函数图象于点R.若y′=PQ+PR，点P横坐标为x. $\text{[math]}$ 关于x的图像如图2，其中图像最低点F、G横坐标分别为（ $\text{[math]}$ ， $\text{[math]}$ ）、（ $\text{[math]}$ ， $\text{[math]}$ ）.
  ①求 $\text{[math]}$ 与x之间的函数关系式.
  ②写出该函数的两条性质.
3. （3）已知1<x<4
  ①若关于x的方程x²－4x－m=0有解，求m的取值范围.小明思考过程如下：由x²－4x－m=0得m=x²－4x，m是关于x的二次函数，根据x的范围可以求出m的取值范围.请你完成解题过程.
  ②若关于x的方程 $\text{[math]}$ 有解，请直接写出m的取值范围.
答案解析收藏纠错 + 选题
15. (2023·松北模拟) 如图，在平面直角坐标系中，直线BC的解析式为 $\text{[math]}$ ，直线BC交x轴和y轴分别于点B和点C，抛物线 $\text{[math]}$ 交x轴于点A和点B，交y轴于点C．
1. （1）求抛物线的解析式；
2. （2）点P是第二象限抛物线上的点，连接PB、PC，设点P的横坐标为t， $\text{[math]}$ 的面积为S．求S与t的函数关系式（不要求写出t的取值范围）；
3. （3）在（2）的条件下，点D在线段 $\text{[math]}$ 上，连接PD、CD， $\text{[math]}$ ，点F在线段BC上， $\text{[math]}$ ， FE的延长线交x轴于点G，交PD于点E，连接CE，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求点P的横出标．
答案解析收藏纠错 + 选题
16. (2023·南岗模拟) 如图，在平面直角坐标系中，点О为坐标原点，抛物线 $\text{[math]}$ 交x轴于A，B两点，交y轴于点C，且 $\text{[math]}$ ．
1. （1）求抛物线的解析式；
2. （2）连接 $\text{[math]}$ ，点D是线段 $\text{[math]}$ 上的一个动点，过点D作 $\text{[math]}$ 轴于点E．在线段 $\text{[math]}$ 上截取 $\text{[math]}$ ，过点F作 $\text{[math]}$ 轴，交抛物线于点G，设点D的横坐标为t，点G的纵坐标为d，求d与t之间的函数解析式（不要求写出自变量t的取值范围）；
3. （3）在（2）的条件下，点H是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，过点C作 $\text{[math]}$ ，交线段 $\text{[math]}$ 于点K，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
17. (2023·道里模拟) 已知：在平面直角坐标系中，抛物线 $\text{[math]}$ 的图象交 $\text{[math]}$ 轴于点 $\text{[math]}$ 和点 $\text{[math]}$ （点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），交 $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）如图1，求拋物线的解析式；
2. （2）如图2，点 $\text{[math]}$ 在第四象限的拋物线上，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交抛物线于点 $\text{[math]}$ ，连按 $\text{[math]}$ 并延长交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标；
3. （3）如图3，在（2）的条件下，连接 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 间的拋物线上，连接 $\text{[math]}$ ，点 $\text{[math]}$ 在y轴上，连接 $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，求直线 $\text{[math]}$ 的解折式．
答案解析收藏纠错 + 选题
18. (2023·兴化模拟) 已知：如图，抛物线 $\text{[math]}$ 经过原点 $\text{[math]}$ ，它的对称轴为直线 $\text{[math]}$ ，动点 $\text{[math]}$ 从抛物线的顶点 $\text{[math]}$ 出发，在对称轴上以每秒 $\text{[math]}$ 个单位的速度向下运动，设动点 $\text{[math]}$ 运动的时间为 $\text{[math]}$ 秒，连接 $\text{[math]}$ 并延长交抛物线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求抛物线解析式及顶点坐标；
2. （2）当三点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 构成以为 $\text{[math]}$ 为斜边的直角三角形时，求 $\text{[math]}$ 的值；
3. （3）将 $\text{[math]}$ 沿直线 $\text{[math]}$ 折叠后，那么点 $\text{[math]}$ 的对称点 $\text{[math]}$ 能否恰好落在坐标轴上？若能，请直接写出所有满足条件的 $\text{[math]}$ 的值；若不能，请说明理由.
答案解析收藏纠错 + 选题
19. (2023·苏州模拟) 如图，已知抛物线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为常数， $\text{[math]}$ ）交 $\text{[math]}$ 轴于 $\text{[math]}$ 、 $\text{[math]}$ 两点，交 $\text{[math]}$ 轴于 $\text{[math]}$ ，将该抛物线位于直线 $\text{[math]}$ （ $\text{[math]}$ 为常数， $\text{[math]}$ ）下方的部分沿直线 $\text{[math]}$ 翻折，其余部分不变，得到的新图像记为“图像 $\text{[math]}$ ”.
1. （1）求该抛物线的解析式；
2. （2）若 $\text{[math]}$ 时，直线 $\text{[math]}$ 与图像 $\text{[math]}$ 有三个交点，求 $\text{[math]}$ 的值；
3. （3）若直线 $\text{[math]}$ 与图像 $\text{[math]}$ 有四个交点，直接写出 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
20. (2023九上·邳州期末) 如图，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ ，与y轴交于点C.
1. （1）求抛物线的表达式：
2. （2）在对称轴上找一点D，使 $\text{[math]}$ 的周长最小，求点D的坐标；
3. （3）点P是抛物线对称轴上的一点，点M是对称轴右侧抛物线上的一点，当 $\text{[math]}$ 是以 $\text{[math]}$ 为腰的等腰直角三角形时，请直接写出所有点M的坐标.
答案解析收藏纠错 + 选题
21. (2023·安徽模拟) 如图1，抛物线 $\text{[math]}$ 与x轴交于A、B两点，与y轴交于点C．
1. （1）求抛物线的顶点纵坐标的最小值；
2. （2）若 $\text{[math]}$ ，点P为抛物线上一点，且在A、B两点之间运动．
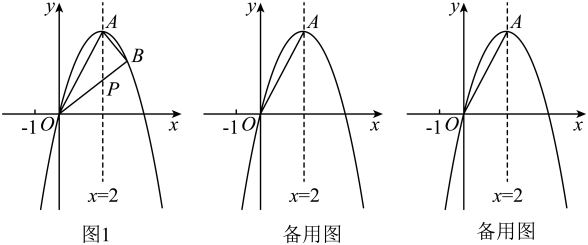
  ①是否存在点Р使得 $\text{[math]}$ ，若存在，求出点P坐标，若不存在，请说明理由；
  ②如图2，连接 $\text{[math]}$ ， $\text{[math]}$ 相交于点M，当 $\text{[math]}$ 的值最大时，求直线 $\text{[math]}$ 的表达式．
答案解析收藏纠错 + 选题
22. (2023·泉州模拟) 在平面直角坐标系 $\text{[math]}$ 中，已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 两点，交y轴于点C，顶点为E.过线段 $\text{[math]}$ 上动点F作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 于点D，直线 $\text{[math]}$ 交y轴于点G.
1. （1）求抛物线的解析式；
2. （2）若 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长；
3. （3）连接 $\text{[math]}$ ，求 $\text{[math]}$ 面积的最小值.
答案解析收藏纠错 + 选题
23. (2023九上·三明模拟) 在平面直角坐标系中， $\text{[math]}$ 为坐标原点，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 在抛物线上.
1. （1）求抛物线的表达式；
2. （2）如图①，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，且点 $\text{[math]}$ 在点 $\text{[math]}$ 的下方，若 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标；
3. （3）如图②， $\text{[math]}$ 为线段 $\text{[math]}$ 上的动点，射线 $\text{[math]}$ 与线段 $\text{[math]}$ 交于点 $\text{[math]}$ ，与抛物线交于点 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
24. (2023·吴兴模拟) 一张矩形纸片ABCD（如图1），AB=6，AD=3.点E是BC边上的一个动点，将△ABE沿直线AE折叠得到△AEF，延长AE交直线CD于点G，直线AF与直线CD交于点Q.

【初步探究】
1. （1）求证：△AQG是等腰三角形；
2. （2）记FQ=m，当BE=2CE时，计算m的值；
3. （3）【深入探究】
  将矩形纸片放入平面直角坐标系中（如图2所示），点B与点O重合，边OC、OA分别与x轴、y轴正半轴重合.点H在OC边上，将△AOH沿直线AH折叠得到△APH.
  ①当AP经过CD的中点N时，求点P的坐标；
  ②在①的条件下，已知二次函数y=-x²+bx+c的图象经过A、D两点.若将直线AH右侧的抛物线沿AH对折，交y轴于点M，请求出AM的长度.
答案解析收藏纠错 + 选题
25. (2023·金华模拟) 如图，抛物线y=-x²+bx+c经过点B（3，0），点C（0，3），D为抛物线的顶点．
1. （1）求抛物线的表达式；
2. （2）在抛物线的对称轴上找一点Q，使∠AQC=90°，求点Q的坐标；
3. （3）在坐标平面内找一点P，使△OCD与△CBP相似，且∠COD=∠BCP，求出所有点P的坐标．
答案解析收藏纠错 + 选题