【备考2024】真题变式分层练：第17题—2023年高考数学...

更新时间：2023-10-03 浏览次数：75 类型：二轮复习

一、原题

1. (2023·全国乙卷) 某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应，进行10次配对试验，每次配对试验选用材质相同的两个橡胶产品，随机地选其中一个用甲工艺处理，另一个用乙工艺处理，测量处理后的橡胶产品的伸缩率，甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为 $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ ），试验结果如下

试验序号i	1	2	3	4	5	6	7	8	9	10
伸缩率 $\text{[math]}$	545	533	551	522	575	544	541	568	596	548
伸缩率 $\text{[math]}$	536	527	543	530	560	533	522	550	576	536

记 $\text{[math]}$ ，记 $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 的样本平均数为 $\text{[math]}$ ，样本方差为 $\text{[math]}$ ，

（1）求 $\text{[math]}$ ， $\text{[math]}$ ；
（2）判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高（如果 $\text{[math]}$ ，则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高，否则不认为有显著提高）.

答案解析收藏纠错 + 选题

二、基础

2. (2023高二上·昆明开学考) 从某小区抽取100户居民用户进行月用电量调查，发现他们的用电量都在50~350(单位： $\text{[math]}$ )之间，进行适当分组后(每组为左闭右开的区间)，画出频率分布直方图如图所示：
1. （1）求在被调查的用户中，用电量落在区间 $\text{[math]}$ 的户数；
2. （2）求直方图中 $\text{[math]}$ 的值；
3. （3）求这组数据的平均数.
答案解析收藏纠错 + 选题

3. (2023高一下·马鞍山期末) 某小学对在校学生开展防震减灾教育，进行一段时间的展板学习和网络学习后，学校对全校学生进行问卷测试（满分 $\text{[math]}$ 分）．现随机抽取了部分学生的答卷，得分的频数统计表和对应的频率分布直方图如图所示：

得分	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
人数	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

（1）求 $\text{[math]}$ ， $\text{[math]}$ 的值，并估计全校学生得分的平均数；
（2）根据频率分布直方图，估计样本数据的 $\text{[math]}$ 和 $\text{[math]}$ 分位数．

答案解析收藏纠错 + 选题

4. (2023高一下·广州期末) 为了解某市今年高一年级学生的身体素质状况，从该市高一年级学生中抽取100名学生进行“掷实心球”的项目测试.经统计，成绩均在2米到12米之间，把获得的所有数据分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成五组，得到频率分布直方图如图所示.
1. （1）根据频率分布直方图，估计该市今年高一年级学生“掷实心球”成绩的平均数（同一组中的数据以该组区间的中点值作代表）；
2. （2）已知这100名学生中有女生40名，男生60名，这40名女生“掷实心球”成绩的平均数和方差分别为7和2.1，这60名男生“掷实心球”成绩的平均数和方差分别为8.5和2.4，求这100名学生“掷实心球”成绩的方差.
答案解析收藏纠错 + 选题
5. (2023高一下·天河期末) 某电子商务公司对10000名网络购物者2023年第一季度的消费情况进行统计，发现消费金额（单位：万元）都在区间 $\text{[math]}$ 内，其频率分布直方图如图所示.
1. （1）求频率直方图中a的值，并估计这些网络购物者第一季度消费金额的平均数；
2. （2）该电子商务公司决定对消费金额高的前18%的消费者进行奖励，若小明的消费金额是0.65万元，请你估算他会得到奖励吗？
答案解析收藏纠错 + 选题
6. (2023高一下·黔西期末) 中学阶段是学生身体发育最重要的阶段，长时间熬夜学习严重影响学生的身体健康．某校为了解甲、乙两班学生每周自我熬夜学习的总时长（单位：小时），分别从这两个班中随机抽取5名同学进行调查，得到他们最近一周自我熬夜学习的总时长的样本数据：
甲班
8
13
28
32
39
乙班
12
25
26
28
31
如果学生平均每周自我熬夜学习的总时长超过26小时，则称为“过度熬夜”．
1. （1）请根据样本数据，分别估计甲、乙两班的学生平均每周自我熬夜学习时长的平均值；
2. （2）从样本甲、乙两班所有“过度熬夜”的学生中任取2人，求这2人都来自甲班的概率．
答案解析收藏纠错 + 选题
7. (2023高二下·福州期末) 为庆祝建党 $\text{[math]}$ 周年，讴歌中华民族实现伟大复兴的奋斗历程，增进全体党员干部职工对党史的了解 $\text{[math]}$ 某单位组织开展党史知识竞赛活动，以支部为单位参加比赛 $\text{[math]}$ 现把 $\text{[math]}$ 名党员的成绩绘制了频率分布直方图，根据图中数据回答下列问题：
1. （1）求 $\text{[math]}$ 的值及这 $\text{[math]}$ 名党员成绩的众数；
2. （2）若要选取成绩前 $\text{[math]}$ 的党员参加上一级的比赛，则应选取多少分以上的参赛？
答案解析收藏纠错 + 选题

8. (2023高一下·湖州期末) 习近平总书记指出：“要健全社会心理服务体系和疏导机制、危机干预机制，塑造自尊自信、理性平和、亲善友爱的社会心态.”在2022年新冠肺炎疫情防控阻击战中，心理医生的相关心理疏导起到了重要作用.某心理调查机构为了解市民在疫情期间的心理健康状况，随机抽取n位市民进行心理健康问卷调查，按所得评分（满分100分）从低到高将心理健康状况分为四个等级：

调查评分	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
心理等级	有隐患		一般		良好	优秀

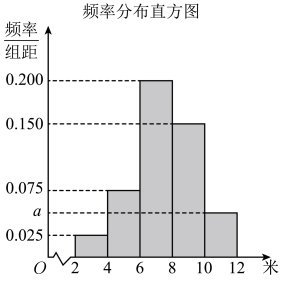
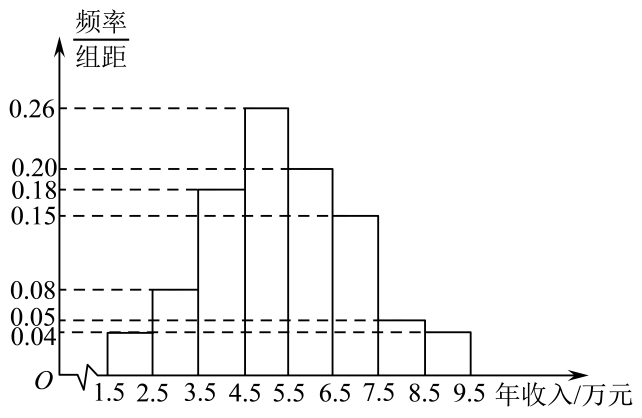
并绘制如图所示的频率分布直方图.已知调查评分在 $\text{[math]}$ 的市民为400人.

（1）求n的值及频率分布直方图中t的值；
（2）在抽取的心理等级为“有隐患”的市民中，按照调查评分分层抽取3人进行心理疏导.据以往数据统计，经过心理疏导后，调查评分在 $\text{[math]}$ 的市民心理等级转为“良好”的概率为 $\text{[math]}$ ，调查评分在 $\text{[math]}$ 的市民心理等级转为“良好”的概率为 $\text{[math]}$ ，若经过心理疏导后的恢复情况相互独立，试问在抽取的3人中，经过心理疏导后，至少有一人心理等级转为“良好”的概率为多少？
（3）心理调查机构与该市管理部门设定的预案是：以抽取的样本作为参考，若市民心理健康指数平均值不低于0.8，则只需发放心理指导资料，否则需要举办心理健康大讲堂.根据你所学的统计知识，判断该市是否需要举办心理健康大讲堂，并说明理由.
注：每组数据以区间的中点值代替，心理健康指数＝问卷调查评分/100.

答案解析收藏纠错 + 选题

9. (2023高一下·广西月考) 射击比赛是群众喜闻乐见的运动形式之一，甲、乙两名射击运动员在某次比赛中各射击6次得到的环数如下表所示：
甲
9
10
6
9
6
8
乙
5
10
10
7
10
6
1. （1）分别求出甲、乙运动员6次射击打出的环数的平均数；
2. （2）分别求出甲、乙运动员这6次射击数据的方差，并根据计算结果说明本次比赛哪位运动员的发挥更稳定．
答案解析收藏纠错 + 选题
10. (2023·全国甲卷) 一项试验旨在研究臭氧效应，试验方案如下：选40只小白鼠，随机地将其中20只分配到试验组，另外20只分配到对照组，试验组的小白鼠饲养在高浓度臭氧环境，对照组的小白鼠饲养在正常环境，一段时间后统计每只小白鼠体重的增加量（单位：g）．试验结果如下：
对照组的小白鼠体重的增加量从小到大排序为

15.2 18.8 20.2 21.3 22.5 23.2 25.8 26.5 27.5 30.1

32.6 34.3 34.8 35.6 35.6 35.8 36.2 37.3 40.5 43.2

试验组的小白鼠体重的增加量从小到大排序为

7.8 9.2 11.4 12.4 13.2 15.5 16.5 18.0 18.8 19.2

19.8 20.2 21.6 22.8 23.6 23.9 25.1 28.2 32.3 36.5
1. （1）计算试验组的样本平均数；
2. （2）（ⅰ）求40只小白鼠体重的增加量的中位数m，再分别统计两样本中小于m与不小于m的数据的个数，完成如下列联表
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  对照组
  
  试验组
  
  （ⅱ）根据（i）中的列联表，能否有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异？
  
  附： $\text{[math]}$ ，
  
  $\text{[math]}$
  
  0.100
  
  0.050
  
  0.010
  
  $\text{[math]}$
  
  2.706
  
  3.841
  
  6.635
答案解析收藏纠错 + 选题
11. (2023高二下·长春期中) 某校对100名高一学生的某次数学测试成绩进行统计，分成 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 五组，得到如图所示频率分布直方图．
1. （1）求图中 $\text{[math]}$ 的值；
2. （2）估计该校高一学生这次数学成绩的众数和平均数；
3. （3）估计该校高一学生这次数学成绩的75%分位数．
答案解析收藏纠错 + 选题
12. (2023·内江模拟) 某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图．为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”．
1. （1）当 $\text{[math]}$ ， $\text{[math]}$ 时，记甲型号电视机的“星级卖场”数量为m，乙型号电视机的“星级卖场”数量为n，比较m，n的大小关系；
2. （2）在这10个卖场中，随机选取2个卖场，记X为其中甲型号电视机的“星级卖场”的个数，求X的分布列和数学期望．
3. （3）记乙型号电视机销售量的方差为 $\text{[math]}$ ，根据茎叶图推断a与b分别取何值时， $\text{[math]}$ 达到最小值．（只需写出结论）
答案解析收藏纠错 + 选题

三、提升

13. (2023高二上·梅河口开学考) 随机抽取100名学生，测得他们的身高（单位： $\text{[math]}$ ），按照区间 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分组，得到样本身高的频率分布直方图如图所示．
1. （1）求频率分布直方图中 $\text{[math]}$ 的值及身高在 $\text{[math]}$ 及以上的学生人数；
2. （2）估计该校100名生学身高的75％分位数．
3. （3）若一个总体划分为两层，通过按样本量比例分配分层随机抽样，各层抽取的样本量、样本平均数和样本方差分别为： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．记总的样本平均数为 $\text{[math]}$ ，样本方差为 $\text{[math]}$ ，证明：
  ① $\text{[math]}$ ；
  
  ② $\text{[math]}$ ．
答案解析收藏纠错 + 选题
14. (2023高三上·开远月考) 《中共中央国务院关于深入打好污染防治攻坚战的意见》提出“构建智慧高效的生态环境管理信息化体系”，下一步，需加快推进5G、物联网、大数据、云计算等新信息技术在生态环境保护领域的建设与应用，实现生态环境管理信息化、数字化、智能化．某科技公司开发出一款生态环保产品，已知该环保产品每售出1件预计利润为0.4万元，当月未售出的环保产品，每件亏损0.2万元．根据市场调研，该环保产品的市场月需求量在 $\text{[math]}$ 内取值，将月需求量区间平均分成5组，画出频率分布直方图如下．
1. （1）请根据频率分布直方图，估计该环保产品的市场月需求量的平均值 $\text{[math]}$ 和方差 $\text{[math]}$ ．
2. （2）若该环保产品的月产量为185件，x（单位：件， $\text{[math]}$ ， $\text{[math]}$ ）表示该产品一个月内的市场需求量，y（单位：万元）表示该公司生产该环保产品的月利润．
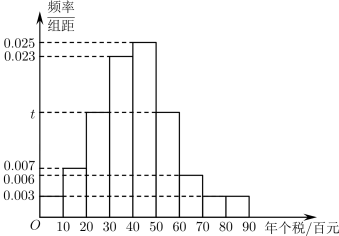
  ①将y表示为x的函数；
  
  ②以频率估计概率，标准差s精确到1，根据频率分布直方图估计 $\text{[math]}$ 且y不少于68万元的概率．
答案解析收藏纠错 + 选题
15. (2023高一下·河南月考) 后疫情时代，为了可持续发展，提高人民幸福指数，国家先后出台了多项减税增效政策．某地区对在职员工进行了个人所得税的调查，经过分层随机抽样，获得2000位在职员工的个人所得税（单位：百元）数据，按 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分成九组，制成如图所示的频率分布直方图：
1. （1）求直方图中t的值：
2. （2）根据频率分布直方图估计该市的70%职工年个人所得税不超过m（百元），求m的最小值；
3. （3）已知该地区有20万在职员工，规定：每位在职员工年个人所得税不超过5000元的正常收取，若超过5000元，则超出的部分退税20%，请估计该地区退税总数约为多少．
答案解析收藏纠错 + 选题
16. (2023高一下·莲湖期末) 某果园大约还有5万个蜜桔等待出售，原销售方案是所有蜜桔都以25元/千克的价格进行销售，为了更好地促进销售，需对蜜桔质量进行质量分析，以便做出合理的促销方案．现从果园内随机采摘200个蜜桔进行测重，其质量分别在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ （单位：克）中，其频率分布直方图如图所示．
1. （1）求m的值；
2. （2）估计该果园这200个蜜桔的平均质量为多少克/个；（同一组的数据以该组区间的中点值为代表）
3. （3）以样本估计总体，若低于55克的蜜桔以140元/百个进行销售，不低于55克的蜜桔以160元/百个进行销售，试问该果园的收益是否会更高？
答案解析收藏纠错 + 选题
17. (2023高一下·台州期末) 第19届亚运会将于2023年9月23日至10月8日在杭州举行，为了弘扬奥林匹克和亚运精神，某学校对全体高中学生组织了一次关于亚运会相关知识的测试.从全校学生中随机抽取了100名学生的成绩作为样本进行统计，测试满分为100分，并将这100名同学的测试成绩分成5组，绘制成了如图所示的频率分布直方图.
1. （1）求频率分布直方图中 $\text{[math]}$ 的值，并估计这100名学生的平均成绩；
2. （2）用样本频率估计总体，如果将频率视为概率，从全校学生中随机抽取3名学生，求3名学生中至少有2人成绩不低于80分的概率.
答案解析收藏纠错 + 选题
18. (2023高一下·番禺期末) 某省实行“ $\text{[math]}$ ”高考模式，为让学生适应新高考的赋分模式，某校在一次校考中使用赋分制给高三年级学生的生物成绩进行赋分，具体赋分方案如下：先按照考生原始分从高到低按比例划定 $\text{[math]}$ 共五个等级，然后在相应赋分区间内利用转换公式进行赋分．其中， $\text{[math]}$ 等级排名占比 $\text{[math]}$ ，赋分分数区间是 $\text{[math]}$ ； $\text{[math]}$ 等级排名占比 $\text{[math]}$ ，赋分分数区间是 $\text{[math]}$ ； $\text{[math]}$ 等级排名占比 $\text{[math]}$ ，赋分分数区间是 $\text{[math]}$ ； $\text{[math]}$ 等级排名占比 $\text{[math]}$ ，赋分分数区间是 $\text{[math]}$ ； $\text{[math]}$ 等级排名占比 $\text{[math]}$ ，赋分分数区间是 $\text{[math]}$ ；现从全年级的生物成绩中随机抽取 $\text{[math]}$ 名学生的原始成绩（未赋分）进行分析，其频率分布直方图如下图：
1. （1）求图中 $\text{[math]}$ 的值；
2. （2）从生物原始成绩为 $\text{[math]}$ 的学生中用分层抽样的方法抽取 $\text{[math]}$ 人，从这 $\text{[math]}$ 人中任意抽取 $\text{[math]}$ 人，求 $\text{[math]}$ 人均在 $\text{[math]}$ 的概率；
3. （3）用样本估计总体的方法，估计该校本次生物成绩原始分不少于多少分才能达到赋分后的 $\text{[math]}$ 等级及以上（含 $\text{[math]}$ 等级）？（结果保留整数）
答案解析收藏纠错 + 选题

19. (2023高一下·金华期末) 树人中学 $\text{[math]}$ 名师生参加了对学校教学管理满意度的评分调查，按样本量比例分配的分层随机抽样方法，抽取 $\text{[math]}$ 个师生的评分（满分 $\text{[math]}$ 分），绘制如图所示的频率分布直方图，并将分数从低到高分为四个等级：

满意度评分	低于 $\text{[math]}$ 分	$\text{[math]}$ 分到 $\text{[math]}$ 分	$\text{[math]}$ 分到 $\text{[math]}$ 分	$\text{[math]}$ 分及以上
满意度等级	不满意	基本满意	满意	非常满意

（1）求图中 $\text{[math]}$ 的值；
（2）若师生的满意指数不低于 $\text{[math]}$ ，则该校可获评“教学管理先进单位”，根据你所学的统计知识，判断该校是否能获奖，并说明理由.（注：满意指数 $\text{[math]}$ ）
（3）假设在样本中，学生、教师的人数分别为 $\text{[math]}$ 、 $\text{[math]}$ .记所有学生的评分为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，其平均数为 $\text{[math]}$ ，方差为 $\text{[math]}$ ，所有教师的评分为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，其平均数为 $\text{[math]}$ ，方差为 $\text{[math]}$ ，总样本评分的平均数为 $\text{[math]}$ ，方差为 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，试估计该校等级为满意的学生的最少人数.

答案解析收藏纠错 + 选题

20. (2023高一下·定远期末) 某市为广泛开展垃圾分类的宣传、教育和倡导工作，使市民树立垃圾分类的环保意识，学会垃圾分类的知识，特举办了“垃圾分类知识竞赛” $\text{[math]}$ 据统计，在为期1个月的活动中，共有两万人次参与网络答题．市文明实践中心随机抽取 $\text{[math]}$ 名参与该活动的市民，以他们单次答题得分作为样本进行分析，由此得到如图所示的频率分布直方图：

（1）求图中 $\text{[math]}$ 的值及参与该活动的市民单次挑战得分的平均成绩 $\text{[math]}$ 同一组中数据用该组区间中点值作代表 $\text{[math]}$ ；
（2）若垃圾分类答题挑战赛得分落在区间 $\text{[math]}$ 之外，则可获得一等奖奖励，其中 $\text{[math]}$ ， $\text{[math]}$ 分别为样本平均数和样本标准差，计算可得 $\text{[math]}$ ，若某人的答题得分为 $\text{[math]}$ 分，试判断此人是否获得一等奖；

（3）为扩大本次“垃圾分类知识竞赛”活动的影响力，市文明实践中心再次组织市民组队参场有奖知识竞赛，竞赛共分五轮进行，已知“光速队”与“超能队”五轮的成绩如表：

成绩	第一轮	第二轮	第三轮	第四轮	第五轮
“光速队”	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
“超能队”	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

$\text{[math]}$ 分别求“光速队”与“超能队”五轮成绩的平均数和方差；

$\text{[math]}$ 以上述数据为依据，你认为“光速队”与“超能队”的现场有奖知识竞赛成绩谁更稳定？

答案解析收藏纠错 + 选题

21. (2023高二下·玉林期中) 全民健身旨在全面提高国民体质和健康水平，倡导全民做到每天参加一次以上的健身活动，学会两种以上健身方法，每年进行一次体质测定．为响应全民健身号召，某单位在职工体测后就某项健康指数（百分制）随机抽取了30名职工的体测数据作为样本进行调查，具体数据如茎叶图所示，其中有1名女职工的健康指数的数据模糊不清（用x表示），已知这30名职工的健康指数的平均数为76.2．
1. （1）根据茎叶图，求样本中男职工健康指数的众数和中位数；
2. （2）根据茎叶图，按男女用分层抽样从这30名职工中随机抽取5人，再从抽取的5人中随机抽取2人，求抽取的2人都是男职工的概率；
3. （3）经计算，样本中男职工健康指数的平均数为81，女职工现有数据（即剔除x）健康指数的平均数为69，方差为190，求样本中所有女职工的健康指数的平均数和方差（结果精确到0.1）．
答案解析收藏纠错 + 选题
22. (2023·德阳模拟) 某学校高二年级某学科的教师决定帮助本年级100名对该科学习困难的学生.为了做到精准帮助，教师对这100名学生的学习兴趣、学习态度、学习习惯等进行调查，并把调查结果转化为各学生的学困指标x，将指标x分成 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 五组，得到如图所示的频率分布直方图.规定若 $\text{[math]}$ ，则认定该生为“绝对学困生”，否则认定该生为“相对学困生”；当 $\text{[math]}$ 时，认定该生为“亟待帮助生”.
1. （1）分别求出“绝对学困生”，“亟待帮助生”的人数；并求学困指标的平均值.
2. （2）在学困指标处于 $\text{[math]}$ 内的学困生中，随机选取两名，用X表示所选两名学生中“亟待帮助生”的人数，求X的分布列和数学期望 $\text{[math]}$ .
答案解析收藏纠错 + 选题
23. (2023·黄山模拟) 为了深入学习领会党的二十大精神，某高级中学全体学生参加了《二十大知识竞赛》，试卷满分为100分，所有学生成绩均在区间 $\text{[math]}$ 分内，已知该校高一､高二､高三年级的学生人数分别为800､1000､1200现用分层抽样的方法抽取了300名学生的答题成绩，绘制了如下样本频率分布直方图.
年级
样本平均数
样本方差
高一
60
75
高二
63
$\text{[math]}$
高三
55
1. （1）根据样本频率分布直方图估计该校全体学生成绩的众数､平均数､第71百分位数；
2. （2）已知所抽取各年级答题成绩的平均数､方差的数据如下表，且根据频率分布直方图估计出总成绩的方差为140，求高三年级学生成绩的平均数 $\text{[math]}$ ，和高二年级学生成绩的方差 $\text{[math]}$ .
答案解析收藏纠错 + 选题

四、培优

24. (2023高一下·合肥期末) 随着老年人消费需求从“生存型”向“发展型”转变．消费层次不断提升，“银发经济”成为社会热门话题之一，被各企业持续关注.某企业为了解该地老年人消费能力情况，对该地年龄在 $\text{[math]}$ 的老年人的年收入按年龄 $\text{[math]}$ ， $\text{[math]}$ 分成两组进行分层抽样调查，已知抽取了年龄在 $\text{[math]}$ 的老年人500人．年龄在 $\text{[math]}$ 的老年人300人．现作出年龄在 $\text{[math]}$ 的老年人年收入的频率分布直方图（如下图所示）．
1. （1）根据频率分布直方图，估计该地年龄在 $\text{[math]}$ 的老年人年收入的平均数及第95百分位数；
2. （2）已知年龄在 $\text{[math]}$ 的老年人年收入的方差为3，年龄在 $\text{[math]}$ 的老年人年收入的平均数和方差分别为3.75和1.4，试估计年龄在 $\text{[math]}$ 的老年人年收入的方差．
答案解析收藏纠错 + 选题
25. (2023高一下·达州期末) 2023年某省参加学业水平测试的高一学生有80万人，现随机抽1万名学生的地理成绩（所有成绩均为整数分）进行统计得到频率分布直方图．
1. （1）根据该图估计这次地理成绩的众数和平均数：
2. （2）学业水平测试划分A，B，C，D四个等级，其中A，B，C等级为合格，D等级为不合格，单科成绩合格比例为95%．若学生甲本次的地理成绩为60分，该学生本次地理成绩是否合格?
答案解析收藏纠错 + 选题
26. (2023·赣州模拟) 近年来，我国加速推行垃圾分类制度，全国垃圾分类工作取得积极进展.某城市推出了两套方案，并分别在 $\text{[math]}$ ， $\text{[math]}$ 两个大型居民小区内试行．方案一：进行广泛的宣传活动，通过设立宣传点、发放宣传单等方式，向小区居民和社会各界宣传垃圾分类的意义，讲解分类垃圾桶的使用方式，垃圾投放时间等，定期召开垃圾分类会议和知识宣传教育活动；方案二：智能化垃圾分类，在小区内分别设立分类垃圾桶，垃圾回收前端分类智能化，智能垃圾桶操作简单，居民可以通过设备进行自动登录、自动称重、自动积分等一系列操作．建立垃圾分类激励机制，比如，垃圾分类换积分，积分可兑换礼品等，激发了居民参与垃圾分类的热情，带动居民积极主动地参与垃圾分类．经过一段时间试行之后，在这两个小区内各随机抽取了100名居民进行问卷调查，记录他们对试行方案的满意度得分（满分100分），将数据分成6组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，并整理得到如下频率分布直方图：
1. （1）请通过频率分布直方图分别估计两种方案满意度的平均得分，判断哪种方案的垃圾分类推广措施更受居民欢迎（同一组中的数据用该组中间的中点值作代表）；
2. （2）以样本频率估计概率，若满意度得分不低于70分说明居民赞成推行此方案，低于70分说明居民不太赞成推行此方案.现从 $\text{[math]}$ 小区内随机抽取5个人，用 $\text{[math]}$ 表示赞成该小区推行方案的人数，求 $\text{[math]}$ 的分布列及数学期望．
答案解析收藏纠错 + 选题
27. (2023·张家界模拟) 2022年底，新冠病毒肆虐全国，很多高三同学也都加入羊羊行列．某校参加某次大型考试时采用了线上考试和线下考试两种形式．现随机抽取200名同学的数学成绩做分析，其中线上人数占40%，线下人数占60%，通过分别统计他们的数学成绩得到了如下两个频率分部直方图：
其中 $\text{[math]}$ 称为合格， $\text{[math]}$ 称为中等， $\text{[math]}$ 称为良好， $\text{[math]}$ 称为优秀， $\text{[math]}$ 称为优异．
1. （1）根据频率分布直方图，求这200名学生的数学平均分（同一组数据可取该组区间的中点值代替）；
2. （2）现从这200名学生中随机抽取一名同学的数学成绩为良好，试分析他是来自线上考试的可能性大，还是来自线下考试的可能性大．
3. （3）现从线下考试的学生中随机抽取10名同学，且抽到k个学生的数学成绩为中等的可能性最大，试求k的值．
答案解析收藏纠错 + 选题
28. 希望种子公司销售一种新品种蔬菜种子，其说明书标明：此品种蔬菜果实的平均长度为11.5cm．某种植大户购买了这种蔬菜种子，种植后从收获的蔬菜果实中随机选取了一个容量为20的样本，得到果实长度数据如下表：（单位：cm）
序号（i）
1
2
3
4
5
6
7
8
9
10
长度 $\text{[math]}$
11.6
13.0
12.8
11.8
12.0
12.8
11.5
12.7
13.4
12.4

序号（i）
11
12
13
14
15
16
17
18
19
20
长度 $\text{[math]}$
12.9
12.8
13.2
13.5
11.2
12.6
11.8
12.8
13.2
12.0
参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）估计该种植大户收获的蔬菜果实长度的平均数 $\text{[math]}$ 和方差 $\text{[math]}$ ；
2. （2）判断说明书标明的“蔬菜果实的平均长度为11.5cm”的说法是否成立．
  （记 $\text{[math]}$ ，其中 $\text{[math]}$ 为蔬菜果实长度的平均数，s为蔬菜果实长度的标准差，n是选取蔬菜果实的个数．当 $\text{[math]}$ 时， $\text{[math]}$ ．若 $\text{[math]}$ ，则说明书标明的“蔬菜果实的平均长度为11.5cm”的说法不成立）
答案解析收藏纠错 + 选题
29. (2023·白山模拟) 2023年，全国政协十四届一次会议于3月4日下午3时在人民大会堂开幕，3月11日下午闭幕，会期7天半；十四届全国人大一次会议于3月5日上午开幕，13日上午闭幕，会期8天半.为调查学生对两会相关知识的了解情况，某高中学校开展了两会知识问答活动，现从全校参与该活动的学生中随机抽取320名学生，他们的得分（满分100分）的频率分布折线图如下.
参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）若此次知识问答的得分 $\text{[math]}$ ，用样本来估计总体，设 $\text{[math]}$ ， $\text{[math]}$ 分别为被抽取的320名学生得分的平均数和标准差，求 $\text{[math]}$ 的值；
2. （2）学校对这些被抽取的320名学生进行奖励，奖励方案如下：用频率估计概率，得分小于或等于55的学生获得1次抽奖机会，得分高于55的学生获得2次抽奖机会.假定每次抽奖抽到价值10元的学习用品的概率为 $\text{[math]}$ ，抽到价值20元的学习用品的概率为 $\text{[math]}$ .从这320名学生中任取一位，记该同学在抽奖活动中获得学习用品的价值总额为 $\text{[math]}$ 元，求 $\text{[math]}$ 的分布列和数学期望（用分数表示），并估算此次抽奖要准备的学习用品的价值总额.
答案解析收藏纠错 + 选题
30. (2023高三下·浙江月考) 大坝是一座具有灌溉、防洪、发电、航运、养殖和游览等综合效益的大型水利枢纽工程．为预测渗压值和控制库水位，工程师在水库选取一支编号为 $\text{[math]}$ 的渗压计，随机收集10个该渗压计管内水位和水库水位监测数据：
样本号 $\text{[math]}$
1
2
3
4
5
6
7
8
9
10
总和
水库水位 $\text{[math]}$
75.69
75.74
75.77
75.78
75.81
75.85
75.67
75.87
75.9
75.93
758.01
$\text{[math]}$ 渗压计管内水位 $\text{[math]}$
72.88
72.90
72.92
72.92
72.93
72.94
72.94
72.95
72.96
72.98
729.32
并计算得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
附：相关系数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）估计该水库中 $\text{[math]}$ 号渗压计管内平均水位与水库的平均水位；
2. （2）求该水库 $\text{[math]}$ 号渗压计管内水位与水库水位的样本相关系数（精确到0.01）；
3. （3）某天雨后工程师测量了水库水位，并得到水库的水位为 $\text{[math]}$ ．利用以上数据给出此时 $\text{[math]}$ 号渗压计管内水位的估计值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

【备考2024】真题变式分层练：第17题—2023年高考数学...

副标题：

*注意事项：

【备考2024】真题变式分层练：第17题—2023年高考数学...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

$\text{[math]}$	0.100	0.050	0.010
$\text{[math]}$	2.706	3.841	6.635

年级	样本平均数	样本方差
高一	60	75
高二	63	$\text{[math]}$
高三		55

序号（i）	1	2	3	4	5	6	7	8	9	10
长度 $\text{[math]}$	11.6	13.0	12.8	11.8	12.0	12.8	11.5	12.7	13.4	12.4

序号（i）	11	12	13	14	15	16	17	18	19	20
长度 $\text{[math]}$	12.9	12.8	13.2	13.5	11.2	12.6	11.8	12.8	13.2	12.0

样本号 $\text{[math]}$	1	2	3	4	5	6	7	8	9	10	总和
水库水位 $\text{[math]}$	75.69	75.74	75.77	75.78	75.81	75.85	75.67	75.87	75.9	75.93	758.01
$\text{[math]}$ 渗压计管内水位 $\text{[math]}$	72.88	72.90	72.92	72.92	72.93	72.94	72.94	72.95	72.96	72.98	729.32

甲班	8	13	28	32	39
乙班	12	25	26	28	31

甲	9	10	6	9	6	8
乙	5	10	10	7	10	6

	$\text{[math]}$	$\text{[math]}$
对照组
试验组