题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

备考浙教版中考数学题型专项训练反比例函数解答题专练

更新时间：2022-05-31 浏览次数：82 类型：三轮冲刺

一、综合题

1. (2022·青岛模拟) 通过构造恰当的图形，可以对线段长度、图形面积大小等进行比较，直观地得到一些不等关系或最值，这是“数形结合”思想的典型应用．
1. （1）【理解】
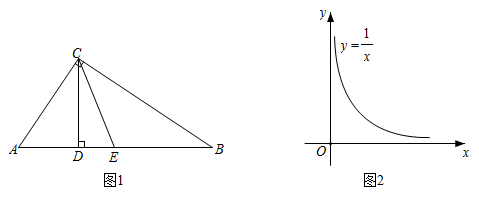
  如图1， $\text{[math]}$ ，垂足分别为C、D，E是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．已知 $\text{[math]}$ ， $\text{[math]}$ ．
  ①分别求线段 $\text{[math]}$ 、 $\text{[math]}$ 的长（用含a、b的代数式表示）；
  ②比较大小： $\text{[math]}$ ▲ $\text{[math]}$ （填“＜”、“＝”或“＞”），并用含a、b的代数式表示该大小关系．
2. （2）【应用】
  如图2，在平面直角坐标系 $\text{[math]}$ 中，点M、N在反比例函数 $\text{[math]}$ 的图像上，横坐标分别为m、n．设 $\text{[math]}$ ，记 $\text{[math]}$ ．
  ①当 $\text{[math]}$ 时， $\text{[math]}$ ▲ ；当 $\text{[math]}$ 时， $\text{[math]}$ ▲ ；
  ②通过归纳猜想，可得l的最小值是 ▲ ．请利用图2构造恰当的图形，并说明你的猜想成立．
答案解析收藏纠错 + 选题
2. (2021九上·金台期末) 如图，在平面直角坐标系中，四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ ，若 $\text{[math]}$ 、 $\text{[math]}$ 的长是关于x的一元二次方程 $\text{[math]}$ 的两个根，且 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 、 $\text{[math]}$ 的长.
2. （2）若点E为x轴正半轴上的点，且 $\text{[math]}$ ，求经过D、E两点的直线解析式及经过点D的反比例函数的解析式，并判断 $\text{[math]}$ AOE与 $\text{[math]}$ AOD是否相似.
3. （3）若点M在平面直角坐标系内，则在直线 $\text{[math]}$ 上是否存在点F，使以A、C、F、M为顶点且 $\text{[math]}$ 、 $\text{[math]}$ 为邻边的四边形为菱形？若存在，写出F点的坐标，若不存在，请说明理由.
答案解析收藏纠错 + 选题
3. (2021九上·枣庄月考) 如图，一次函数y＝ax﹣1的图象与反比例函数 $\text{[math]}$ 的图象交于A，B两点，与x轴交于点C，与y轴交于点D，已知OA＝ $\text{[math]}$ ， tan∠AOC＝ $\text{[math]}$
1. （1）求a，k的值及点B的坐标；
2. （2）观察图象，请直接写出不等式ax﹣1≥ $\text{[math]}$ 的解集；
3. （3）在y轴上存在一点P，使得△PDC与△ODC相似，请你求出P点的坐标．
答案解析收藏纠错 + 选题
4. (2021九上·上高月考) 如图，矩形ABCD的两边AD、AB的长分别为3、8，边BC落在x轴上，E是DC的中点，连接AE．
1. （1）若点B坐标为（﹣6，0），求直线AE的表达式；
2. （2）反比例函数y＝ $\text{[math]}$ （x＜0）的图象经过点E，与AB交于点F，若AF﹣AE＝2，求反比例函数的表达式；
3. （3）在（2）的条件下，连接矩形ABCD两对边AD与BC的中点M、N，设线段MN与反比例函数图象交于点P，将线段MN沿x轴向右平移n个单位，若MP＜NP，直接写出n的取值范围．
答案解析收藏纠错 + 选题
5. (2021九上·成都月考) 如图，过原点的直线y＝2x交反比例函数y₁＝ $\text{[math]}$ 于B点，交反比例函数y₂＝ $\text{[math]}$ 于C点，且OB＝BC，A点横坐标为4且为y₁＝ $\text{[math]}$ 上一点，过B点作BD⊥x轴，垂足为点D.
1. （1）求反比例函数y₂＝ $\text{[math]}$ 与直线AD的解析式
2. （2）是否反比例函数y₂＝ $\text{[math]}$ 图象在第一象限内存在一点P，使得S_△ABP＝ $\text{[math]}$ S_{四边形ADBP} ，若存在，求出P点坐标；若不存在，请说明理由.
3. （3）若动点Q在图象y₂＝ $\text{[math]}$ 上，在平面内是否存在点H，使得A、B、Q、H四点能组成以AB为边的矩形？若存在，请直接写出H点的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题

6. (2021八上·郑州期末) 为了探索函数y＝x+ $\text{[math]}$ （x＞0）的图象与性质，我们参照学习函数的过程与方法.

列表：

x	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	2	3	4	5	…
y	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	2	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	…

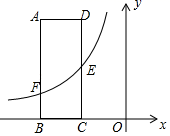
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图1所示：

（1）如图1，观察所描出点的分布，用一条光滑曲线将点顺次连接起来，作出函数图象；
（2）已知点（x₁ ， y₁），（x₂ ， y₂）在函数图象上，结合表格和函数图象，回答下列问题：
若0＜x₁＜x₂≤1，则y₁y₂；若1＜x₁＜x₂ ，则y₁y₂；

若x₁•x₂＝1，则y₁y₂（填“＞”，“＝”或“＜”）.
（3）某农户要建造一个图2所示的长方体形无盖水池，其底面积为1平方米，深为1米.已知底面造价为1千元/平方米，侧面造价为0.5千元/平方米.设水池底面一边的长为x米，水池总造价为y千元.
①请写出y与x的函数关系式；

②若该农户预算不超过3.5千元，请直接写出水池底面一边的长x的取值范围.

答案解析收藏纠错 + 选题

7. (2022·东平模拟) 如图，一次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与反比例函数 $\text{[math]}$ 的图象交于B，D两点，且AC=BC.
1. （1）求反比例函数的解析式；
2. （2）已知 $\text{[math]}$ 是 $\text{[math]}$ 轴正半轴上一点，作 $\text{[math]}$ 轴交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，交双曲线于点 $\text{[math]}$ ，当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形为平行四边形时，请写出点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
8. (2021九上·罗湖期中) 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象相交于 $\text{[math]}$ 两点，其中点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点B的坐标为 $\text{[math]}$ ．
1. （1）求这两个函数的表达式；
2. （2）根据图象，直接写出满足 $\text{[math]}$ 的 $\text{[math]}$ 的取值范围；
3. （3）若点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，使得 $\text{[math]}$ ，请直接写出点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
9. (2021·斗门模拟) 如图，在平面直角坐标系中， $\text{[math]}$ 为坐标原点，点 $\text{[math]}$ 在 $\text{[math]}$ 轴正半轴上，四边形 $\text{[math]}$ 为平行四边形， $\text{[math]}$ ，反比例函数 $\text{[math]}$ 的图象在第一象限内过点 $\text{[math]}$ ，且经过 $\text{[math]}$ 边的中点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求反比例函数的表达式；
2. （2）在（1）的条件下，求点 $\text{[math]}$ 的坐标；
3. （3）证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
10. (2021·沈丘模拟) 如图，在平面直角坐标系中，点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，矩形 $\text{[math]}$ 与坐标轴的交点分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 轴，连接 $\text{[math]}$ ， $\text{[math]}$ ，分别交坐标轴于点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 为定值；
2. （2）若 $\text{[math]}$ 为 $\text{[math]}$ 的中点，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
11. (2021·张店模拟) 已知一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象在第一象限交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求反比例函数与一次函数的解析式；
2. （2）直接写出 $\text{[math]}$ 的解集；
3. （3）若点 $\text{[math]}$ 为 $\text{[math]}$ 轴上一点，求使 $\text{[math]}$ 的点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
12. (2020·永州模拟) 如图，抛物线L： $\text{[math]}$ （常数t＞0）与x轴从左到右的交点为B，A，过线段OA的中点M作MP⊥x轴，交双曲线 $\text{[math]}$ 于点P，且OA·MP=12.
1. （1）求k值；
2. （2）当t=1时，求AB长，并求直线MP与L对称轴之间的距离；
3. （3）把L在直线MP左侧部分的图象（含与直线MP的交点）记为G，用t表示图象G最高点的坐标；
4. （4）设L与双曲线有个交点的横坐标为x₀ ，且满足4≤x₀≤6，通过L位置随t变化的过程，直接写出t的取值范围.
答案解析收藏纠错 + 选题
13. (2020·天台模拟) 如图
1. （1）方法体验：
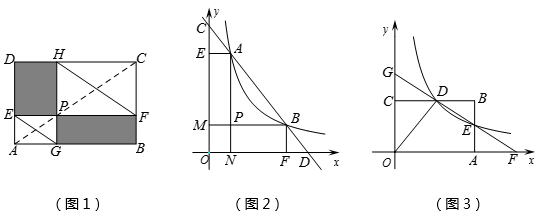
  如图1，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H，容易证明四边形PEDH和四边形PFBG是面积相等的矩形，分别连结EG，FH.
  
  ①根据矩形PEDH和矩形PFBG面积相等的关系，那么PE·PH= ▲ .
  
  ②求证：EG∥FH.
2. （2）方法迁移：
  如图2，已知直线 $\text{[math]}$ 分别与x轴，y轴交于D，C两点，
  
  与双曲线 $\text{[math]}$ 交于A，B两点. 求证：AC=BD.
3. （3）知识应用：
  如图3，反比例函数 $\text{[math]}$ （x＞0）的图象与矩形ABCO的边BC交于点D，与边AB交于点E，直线DE与x轴，y轴分别交于点F，G . 若矩形ABCO的面积为10，△ODG与△ODF的面积比为3：5，则k=.
答案解析收藏纠错 + 选题

14. (2021·重庆市模拟) 在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．我们对函数 $\text{[math]}$ 图象与性质进行探究，下表是该函数y与自变量x的几组对应值，请解答下列问题：

x

…

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

0

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

…

y

…

$\text{[math]}$

$\text{[math]}$

m

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

0

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

n

$\text{[math]}$

$\text{[math]}$

…

（1）求该函数的解析式，并写出自变量x的取值范围．
（2）表中m的值为，n的值为．
（3）在如图所示的平面直角坐标系中，画出该函数的图象，并写出该函数的一条性质；
（4）直接写出关于x的不等式 $\text{[math]}$ 的解集是．（如果取近似值，误差不超过0.2）．

答案解析收藏纠错 + 选题

15. (2021·惠城模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，顶点 $\text{[math]}$ ， $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，直线 $\text{[math]}$ 轴，垂足为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）若 $\text{[math]}$ ，求直线 $\text{[math]}$ 的解析式．
答案解析收藏纠错 + 选题
16. (2021·三台模拟) 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 、 $\text{[math]}$ 两点，与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴分别交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，且点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .
1. （1）求一次函数和反比例函数的表达式.
2. （2）求 $\text{[math]}$ 的面积.
3. （3）点 $\text{[math]}$ 为反比例函数图象上的一个动点， $\text{[math]}$ 轴于 $\text{[math]}$ ，是否存在以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 相似，若存在，直接写出 $\text{[math]}$ 点的坐标，若不存在，请说明理由.
答案解析收藏纠错 + 选题
17. (2019·临海模拟) 知识背景
当a＞0且x＞0时，因为（ $\text{[math]}$ ﹣ $\text{[math]}$ ）²≥0，所以x﹣2 $\text{[math]}$ + $\text{[math]}$ ≥0，从而x+ $\text{[math]}$ （当x= $\text{[math]}$ 时取等号）.

设函数y=x+ $\text{[math]}$ （a＞0，x＞0），由上述结论可知：当x= $\text{[math]}$ 时，该函数有最小值为2 $\text{[math]}$ .

应用举例

已知函数为y₁=x（x＞0）与函数y₂= $\text{[math]}$ （x＞0），则当x= $\text{[math]}$ =2时，y₁+y₂=x+ $\text{[math]}$ 有最小值为2 $\text{[math]}$ =4.

解决问题
1. （1）已知函数为y₁=x+3（x＞﹣3）与函数y₂=（x+3）²+9（x＞﹣3），当x取何值时， $\text{[math]}$ 有最小值？最小值是多少？
2. （2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0.001.若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租货使用成本最低？最低是多少元？
答案解析收藏纠错 + 选题
18. (2019·丹阳模拟) 如图，在平面直角坐标系中，函数 $\text{[math]}$ （ $\text{[math]}$ ，是常数）的图像经过A(2，6)，B(m，n)，其中m>2.过点A作 $\text{[math]}$ 轴垂线，垂足为C，过点 $\text{[math]}$ 作轴垂线，垂足为 $\text{[math]}$ ，AC与BD交于点E，连结AD， $\text{[math]}$ ，CB.
1. （1）若 $\text{[math]}$ 的面积为3，求m的值和直线 $\text{[math]}$ 的解析式；
2. （2）求证： $\text{[math]}$ ；
3. （3）若AD//BC ，求点B的坐标 .
答案解析收藏纠错 + 选题
19. (2019·潮南模拟) 如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（ $\text{[math]}$ ，1）在反比例函数 $\text{[math]}$ 的图象上．
1. （1）求反比例函数 $\text{[math]}$ 的表达式；
2. （2）在x轴的负半轴上存在一点P，使得S_△_AOP= S_△_AOB ，求点P的坐标；
3. （3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．
答案解析收藏纠错 + 选题
20. (2019·广西模拟) 一辆客车从甲地出发前往乙地，平均速度v(千米／小时)与所用时间t(小时)的函数关系如图所示，其中60≤v≤120．
1. （1）直接写出v与t的函数关系式；
2. （2）若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶20千米，3小时后两车相遇．
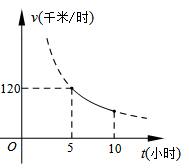
  ①求两车的平均速度；
  
  ②甲、乙两地问有两个加油站A，B，它们相距200千米，当客车进入B加油站时，货车恰好进入A加油站(两车加油的时间忽略不计)，求甲地与B加油站的距离．
答案解析收藏纠错 + 选题
21. (2018·福州模拟) 【阅读理解】对于任意正实数a、b，因为 $\text{[math]}$ ≥0，所以 $\text{[math]}$ $\text{[math]}$ ≥0，所以 $\text{[math]}$ ≥2 $\text{[math]}$ ，只有当 $\text{[math]}$ 时，等号成立．
【获得结论】在 $\text{[math]}$ ≥2 $\text{[math]}$ （a、b均为正实数）中，若 $\text{[math]}$ 为定值 $\text{[math]}$ ，则 $\text{[math]}$ ≥2 $\text{[math]}$ ，只有当 $\text{[math]}$ 时， $\text{[math]}$ 有最小值2 $\text{[math]}$ ．
1. （1）根据上述内容，回答下列问题：若 $\text{[math]}$ >0，只有当 $\text{[math]}$ =时， $\text{[math]}$ 有最小值．
2. （2）【探索应用】如图，已知A（－3，0），B（0，－4），P为双曲线 $\text{[math]}$ （ $\text{[math]}$ ＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．
答案解析收藏纠错 + 选题
22. (2021·大连模拟) 如图，平面直角坐标系中，点C在x轴上，点A的横坐标是1，以OA ， OC为邻边作 $\text{[math]}$ ，点D是BC的中点，反比例函数 $\text{[math]}$ 的图象经过点A ，点D ．
1. （1）求点B的坐标（用含k的代数式表示）；
2. （2）连接AD ，若AB＝AD ，求k的值．
答案解析收藏纠错 + 选题
23. (2021·禹州模拟) 如图，在平面直角坐标系xOy中，菱形ABCD的顶点B的坐标为（1，0），顶点C的坐标为（4，2），对角线AC∥x轴，边AB所在直线y₁＝ax+b与反比例函数y₂＝ $\text{[math]}$ （k＜0）的图象交于A，E两点；
1. （1）求y₁和y₂的函数解析式；
2. （2）当y₁＞y₂时，求x的取值范围；
3. （3）点P是x轴上一动点，当△PAC是以AC为斜边的直角三角形时，请直接写出点P的坐标.
答案解析收藏纠错 + 选题
24. (2021·乾安模拟) 如图，在平面直角坐标系中，正六边 $\text{[math]}$ 的对称中心 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，边 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上．已知 $\text{[math]}$ ．
1. （1）点 $\text{[math]}$ 是否在该反比例函数的图象上？请说明理由．
2. （2）若该反比例函数图象与 $\text{[math]}$ 交于点 $\text{[math]}$ ．求点 $\text{[math]}$ 的横坐标．
答案解析收藏纠错 + 选题
25. (2021·淄川模拟) 如图，在平面直角坐标系xOy中，双曲线y₁＝ $\text{[math]}$ 与直线y₂＝mx＋n交于点A ， E ， AE交x轴于点C ，交y轴于点D ， $\text{[math]}$ 轴于点B，C为OB中点．若D点坐标为（0，﹣2），且S_△AOD＝4
1. （1）求双曲线与直线AE的解析式；
2. （2）写出E点的坐标；
3. （3）观察图象，直接写出y₁≥y₂时x的取值范围．
答案解析收藏纠错 + 选题
26. (2022·婺城模拟) 跳台滑雪是北京冬奥会的比赛项目之一.下图是某跳台滑雪场地的截面示意图. 平台AB长1米（即AB=1），平台AB距地面18米.以地面所在直线为x轴，过点B垂直于地面的直线为y轴，取1米为单位长度，建立平面直角坐标系.已知滑道对应的函数为 $\text{[math]}$ .运动员（看成点）在BA方向获得速度v米/秒后，从A处向右下飞向滑道，点M是下落过程中的某位置（忽略空气阻力）.设运动员飞出时间为t秒，运动员与点A的竖直距离为h米，运动员与点A的水平距离为l米.经实验表明：h=6t² ， l=vt.
1. （1）求k的值；
2. （2）当v=5，t=1时，通过计算判断运动员是否落在滑道上；
3. （3）若运动员甲、乙同时从A处飞出，已知甲离开点A的速度是5米/秒.当甲距x轴4.5米时，乙恰好位于甲右侧4.5米的位置，求t的值与运动员乙离开A的速度.
答案解析收藏纠错 + 选题

27. (2022·上城模拟) 某同学设计了如下杠杆平衡实验：如图，取一根长65cm的质地，均匀木杆，用细绳绑在木杆的中点O处并将其吊起来，在中点的左侧，距离中点20cm处挂一个重9N的物体，在中点的右侧，用一个弹簧测力计向下拉，使木杆保持平衡（动力×动力臂＝阻力×阻力臂），改变弹簧测力计与中点O的距离L（单位：cm），观察弹簧测力计的示数F（单位：N）. 通过实验，得到下表数据：

	第1组	第2组	第3组	第4组	第5组
L/cm	20	24	25	28	30
F/N	9	7.5	10	6

（1）你认为表中哪组数据是明显错误的.
（2）在已学过的函数中选择合适的模型，求F关于L的函数表达式.
（3）若弹簧测力计的量程是10N，求L的取值范围.

答案解析收藏纠错 + 选题

28. (2021·福建模拟) 厨余垃圾无公害化、高效化处理是破解“日益严重的垃圾包围城市的困境”的重要手段之一.某科研团队在自然界中找到了两种“吞噬细菌甲，乙”，并进行实验室繁殖.通过研究，科研人员发现：等数量的吞噬细菌甲、乙分解单位体积内的厨余垃圾的速率v（单位： $\text{[math]}$ ）与环境温度T（单位：℃）存在如图所示的函数关系，分段函数 $\text{[math]}$ 对应吞噬细菌甲、分段函数 $\text{[math]}$ 对应吞噬细菌乙（ $\text{[math]}$ 与 $\text{[math]}$ 的图象中，曲线部分是双曲线，其余均是直线）.
1. （1）根据图中给出的数据，求函数 $\text{[math]}$ ， $\text{[math]}$ 的函数解析式；
2. （2）在测试中，科研人员又发现：若吞噬细菌甲、乙共存，则总分解速率v将会发生改变，对应的函数曲线为 $\text{[math]}$ ，其中，线段 $\text{[math]}$ 是 $\text{[math]}$ 的角平分线，求线段 $\text{[math]}$ 对应的函数解析式.
答案解析收藏纠错 + 选题

29. (2021·孟津模拟) 汛期到来，山洪暴发，下表记录了某水库 $\text{[math]}$ 内水位的变化情况，其中 $\text{[math]}$ 表示时间（单位： $\text{[math]}$ ）， $\text{[math]}$ 表示水位高度（单位： $\text{[math]}$ ），当 $\text{[math]}$ （ $\text{[math]}$ ）时，达到警戒水位，开始开闸放水.

$\text{[math]}$	0	2	4	6	8	10	12	14	16	18	20
$\text{[math]}$	14	15	16	17	18	14.4	12	10.3	9	8	7.2

（1）在给出的平面直角坐标系中，根据表格中的数据画出水位变化图象，并写出水位高出16米的时间 $\text{[math]}$ 的取值范围 ▲ .（精确到0.1）
（2）请分别求出开闸放水前和放水后最符合表中数据的函数解析式.
（3）据估计，开闸放水后，水位的这种变化规律还会持续一段时间，预测何时水位达到 $\text{[math]}$ .

答案解析收藏纠错 + 选题

30. (2021·拱墅模拟) 如图，小明想要用撬棍撬动一块大石头，已知阻力为 $\text{[math]}$ ，阻力臂长为 $\text{[math]}$ .设动力为y（N），动力臂长为x（m）.（杠杆平衡时，动力×动力臂＝阻力×阻力臂，图中撬棍本身所受的重力略去不计.）
1. （1）求y关于x的函数表达式.
2. （2）当动力臂长为 $\text{[math]}$ 时，撬动石头至少需要多大的力？
3. （3）小明若想使动力不超过 $\text{[math]}$ ，在动力臂最大为 $\text{[math]}$ 的条件下，他能否撬动这块石头？请说明理由.
答案解析收藏纠错 + 选题

试卷信息