2022~2023学年中考数学一轮复习专题13四边形判定与性...

更新时间：2022-12-13 浏览次数：89 类型：一轮复习

一、有关平行四边形的性质与判定

1. (2024八下·象山期中) 如图，在平行四边形ABCD中，点E、F在对角线BD上，且BE＝DF．求证：
1. （1） △ABE≌△CDF；
2. （2）四边形AECF是平行四边形．
答案解析收藏纠错 + 选题
2. (2022·内江) 如图， $\text{[math]}$ 中，E、F是对角线BD上两个点，且满足BE=DF.
1. （1）求证：△ABE≌△CDF；
2. （2）求证：四边形AECF是平行四边形.
答案解析收藏纠错 + 选题
3. (2022·贺州) 如图，在平行四边形ABCD中，点E，F分别在AD，BC上，且 $\text{[math]}$ ，连接AF，CE，AC，EF，且AC与EF相交于点O.
1. （1）求证：四边形AFCE是平行四边形；
2. （2）若AC平分 $\text{[math]}$ ， $\text{[math]}$ ，求四边形AFCE的面积.
答案解析收藏纠错 + 选题
4. (2022·温州) 如图，在△ABC 中， AD⊥BC于点D、E、F分别是AC、AB 的中点，O是 DF 的中点， EO 的延长线交线段 BD 于点G，连结 DE、EF、FG．
1. （1）求证：四边形 DEFG 是平行四边形．
2. （2）当AD=5，tan∠EDC= $\text{[math]}$ =时，求 FG 的长．
答案解析收藏纠错 + 选题
5. (2021·盐城) 如图， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 各边的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 为平行四边形；
2. （2）加上条件 ▲ 后，能使得四边形 $\text{[math]}$ 为菱形，请从① $\text{[math]}$ ；② $\text{[math]}$ 平分 $\text{[math]}$ ；③ $\text{[math]}$ ，这三个条件中选择条件填空（写序号），并加以证明.
答案解析收藏纠错 + 选题
6. (2021·鄂州) 如图，在 $\text{[math]}$ 中，点E、F分别在边 $\text{[math]}$ 、 $\text{[math]}$ 上，且 $\text{[math]}$ .
1. （1）探究四边形 $\text{[math]}$ 的形状，并说明理由；
2. （2）连接 $\text{[math]}$ ，分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点G、H，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点O.若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题

二、有关菱形的性质与判定

7. (2022九下·南平期中) 如图，在菱形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点E为边AB上一个动点，延长BA到点F ，使 $\text{[math]}$ ，且CF、DE相交于点G
1. （1）当点E运动到AB中点时，证明：四边形DFEC是平行四边形；
2. （2）当 $\text{[math]}$ 时，求AE的长；
3. （3）当点E从点A开始向右运动到点B时，求点G运动路径的长度．
答案解析收藏纠错 + 选题
8. (2022·衢州) 如图，在菱形ABCD中，AB=5，BD为对角线.点E是边AB延长线上的任意一点，连结DE交BC于点F，BG平分∠CBE交DE于点G．
1. （1）求证： $\text{[math]}$ .
2. （2）若 $\text{[math]}$ ．
  ①求菱形 $\text{[math]}$ 的面积.
  
  ②求 $\text{[math]}$ 的值.
3. （3）若 $\text{[math]}$ ，当 $\text{[math]}$ 的大小发生变化时（ $\text{[math]}$ ），在AE上找一点T，使GT为定值，说明理由并求出ET的值．
答案解析收藏纠错 + 选题
9. (2022·广州) 如图，在菱形ABCD中，∠BAD = 120°，AB = 6，连接BD ．
1. （1）求BD的长；
2. （2）点E为线段BD上一动点（不与点B，D重合），点F在边AD上，且BE= $\text{[math]}$ DF，
  ①当CE丄AB时，求四边形ABEF的面积；
  
  ②当四边形ABEF的面积取得最小值时，CE+ $\text{[math]}$ CF的值是否也最小？如果是，求CE+ $\text{[math]}$ CF的最小值；如果不是，请说明理由．
答案解析收藏纠错 + 选题
10. (2022·连云港) 如图，四边形 $\text{[math]}$ 为平行四边形，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 为菱形；
2. （2）若 $\text{[math]}$ 是边长为2的等边三角形，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别在线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 上运动，求 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
11. (2022·安徽) 已知四边形ABCD中，BC＝CD．连接BD，过点C作BD的垂线交AB于点E，连接DE．
1. （1）如图1，若 $\text{[math]}$ ，求证：四边形BCDE是菱形；
2. （2）如图2，连接AC，设BD，AC相交于点F，DE垂直平分线段AC．
  （ⅰ）求∠CED的大小；
  （ⅱ）若AF＝AE，求证：BE＝CF．
答案解析收藏纠错 + 选题
12. (2022八上·岷县开学考) 如图，在▱ $\text{[math]}$ 中，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径画弧交 $\text{[math]}$ 于点 $\text{[math]}$ ，再分别以点 $\text{[math]}$ 、 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的相同长为半径画弧，两弧交于点 $\text{[math]}$ ；连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）根据以上尺规作图的过程，证明四边形 $\text{[math]}$ 是菱形；
2. （2）若菱形 $\text{[math]}$ 的边长为 $\text{[math]}$ ， $\text{[math]}$ ，求菱形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题

三、有关矩形的性质与判定

13. (2023·汨罗一模) 如图，▱ABCD中，E为BC边的中点，连接AE并延长交DC的延长线于点F，延长EC至点G，使CG=CE，连接DG、DE、FG．
1. （1）求证：△ABE≌△FCE；
2. （2）若AD=2AB，求证：四边形DEFG是矩形．
答案解析收藏纠错 + 选题
14. (2023八下·盐都期中) 如图，线段DE与AF分别为△ABC的中位线与中线.
1. （1）求证：AF与DE互相平分；
2. （2）当线段AF与BC满足怎样的数量关系时，四边形ADFE为矩形？请说明理由.
答案解析收藏纠错 + 选题
15. (2022·云南) 如图，在平行四边形ABCD中，连接BD，E为线段AD的中点，延长BE与CD的延长线交于点F，连接AF，∠BDF=90°
1. （1）求证：四边形ABDF是矩形；
2. （2）若AD=5，DF=3，求四边形ABCF的面积S．
答案解析收藏纠错 + 选题
16. (2023·丽江模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点.
1. （1）求证： $\text{[math]}$ ；
2. （2）设 $\text{[math]}$ ，当 $\text{[math]}$ 为何值时，四边形 $\text{[math]}$ 是矩形？请说明理由.
答案解析收藏纠错 + 选题
17. (2024九下·新市区开学考) 如图1，△ABC是等腰直角三角形，AC=BC=4，∠C=90°，M，N分别是边AC，BC上的点，以CM，CN为邻边作矩形PMCN，交AB于E，F．设CM=a，CN=b，若ab=8．
1. （1）判断由线段AE，EF，BF组成的三角形的形状，并说明理由；
2. （2） ①当a=b时，求∠ECF的度数；
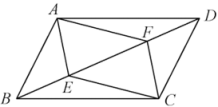
  ②当a≠b时，①中的结论是否成立？并说明理由．
答案解析收藏纠错 + 选题
18. (2022·绍兴) 如图，在矩形 ABCD中，AB=6，BC=8，动点 E从点A出发，沿边AD，DC向点C运动，A， D关于直线 BE的对称点分别为M，N，连结MN ．
1. （1）如图，当E在边AD上且 DE=2时，求 ∠AEM的度数．
2. （2）当N在BC延长线上时，求DE的长，并判断直线MN与直线BD的位置关系，说明理由．
3. （3）当直线MN恰好经过点 C 时，求DE的长．
答案解析收藏纠错 + 选题
19. (2022·河南) 综合与实践
综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动.
1. （1）操作判断
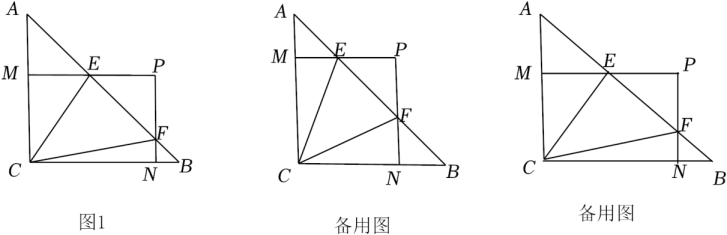
  操作一：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；
  
  操作二：在AD上选一点P，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM，BM.
  
  根据以上操作，当点M在EF上时，写出图1中一个30°的角：.
2. （2）迁移探究
  小华将矩形纸片换成正方形纸片，继续探究，过程如下：
  
  将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q，连接BQ.
  
  ①如图2，当点M在EF上时，∠MBQ＝▲ °，∠CBQ＝▲ °；
  
  ②改变点P在AD上的位置（点P不与点A，D重合），如图3，判断∠MBQ与∠CBQ的数量关系，并说明理由.
3. （3）拓展应用
  在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ＝1cm时，直接写出AP的长.
答案解析收藏纠错 + 选题
20. (2022九上·南关开学考) 如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝OC，BO＝OD，且∠AOB＝2∠OAD.
1. （1）求证：四边形ABCD是矩形；
2. （2）若∠AOB∶∠ODC＝4∶3，求∠ADO的度数.
答案解析收藏纠错 + 选题

四、有关正方形的性质与判定

21. (2023八下·浏阳期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 的角平分线交 $\text{[math]}$ 于点D， $\text{[math]}$ .
1. （1）试判断四边形 $\text{[math]}$ 的形状，并说明理由；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
22. (2023·万山模拟) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ， $\text{[math]}$ 的垂直平分线交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
23. (2023九上·定西月考) 问题解决：如图1，在矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别在 $\text{[math]}$ 边上， $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 是正方形；
2. （2）延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$ ，判断 $\text{[math]}$ 的形状，并说明理由.
  类比迁移：如图2，在菱形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别在 $\text{[math]}$ 边上， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
24. (2021·长春) 实践与探究
1. （1）操作一：如图①，已知正方形纸片ABCD ，将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M ，折痕为AE ，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF ，则 $\text{[math]}$ 度．
2. （2）操作二：如图②，将正方形纸片沿EF继续折叠，点C的对应点为点N ．我们发现，当点E的位置不同时，点N的位置也不同．当点E在BC边的某一位置时，点N恰好落在折痕AE上，则 $\text{[math]}$ 度．
3. （3）在图②中，运用以上操作所得结论，解答下列问题：
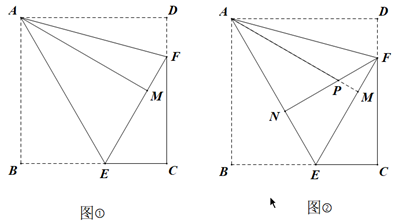
  设AM与NF的交点为点P．求证 $\text{[math]}$ ：．
4. （4）若 $\text{[math]}$ ，则线段AP的长为．
答案解析收藏纠错 + 选题

五、四边形性质与判定综合运用题

25. (2022·镇江) 已知，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别在正方形 $\text{[math]}$ 的边 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 上．
1. （1）如图1，当四边形 $\text{[math]}$ 是正方形时，求证： $\text{[math]}$ ；
2. （2）如图2，已知 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 、 $\text{[math]}$ 的大小有关系时，四边形 $\text{[math]}$ 是矩形；
3. （3）如图3， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ，已知正方形 $\text{[math]}$ 的边长为16， $\text{[math]}$ 长为20，当 $\text{[math]}$ 的面积取最大值时，判断四边形 $\text{[math]}$ 是怎样的四边形？证明你的结论．
答案解析收藏纠错 + 选题
26. (2021·德阳) 如图，点E是矩形ABCD的边BC上一点，将△ABE绕点A逆时针旋转至△AB₁E₁的位置，此时E、B₁、E₁三点恰好共线.点M、N分别是AE和AE₁的中点，连接MN、NB₁.
1. （1）求证：四边形MEB₁N是平行四边形；
2. （2）延长EE₁交AD于点F，若EB₁＝E₁F， $\text{[math]}$ ，判断△AE₁F与△CB₁E是否全等，并说明理由.
答案解析收藏纠错 + 选题
27. (2021·枣庄) 如图1，对角线互相垂直的四边形叫做垂美四边形．
1. （1）概念理解：如图2，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，问四边形 $\text{[math]}$ 是垂美四边形吗？请说明理由；
2. （2）性质探究：如图1，垂美四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ．猜想： $\text{[math]}$ 与 $\text{[math]}$ 有什么关系？并证明你的猜想．
3. （3）解决问题：如图3，分别以 $\text{[math]}$ 的直角边 $\text{[math]}$ 和斜边 $\text{[math]}$ 为边向外作正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
28. (2019·淄博模拟) 如图，正方形 $\text{[math]}$ 和 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 在同一条直线上，且 $\text{[math]}$ ，取 $\text{[math]}$ 的中点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）试证明 $\text{[math]}$ ，并求 $\text{[math]}$ 的值．
2. （2）如图，将如图中的正方形变为菱形，设 $\text{[math]}$ ，其它条件不变，问（1）中 $\text{[math]}$ 的值有变化吗？若有变化，求出该值（用含 $\text{[math]}$ 的式子表示）；若无变化，说明理由．
答案解析收藏纠错 + 选题