人教版初中数学几何辅助线进阶训练——等腰三角形的辅助线（不含...

更新时间：2023-05-03 浏览次数：72 类型：复习试卷

一、一阶段（较易）

1. (2023·内江模拟) 如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB＝60°，DC＝EF.
1. （1）求证：四边形EFCD是平行四边形；
2. （2）若BF＝EF，求证：AE＝AD.
答案解析收藏纠错 + 选题
2. (2023八上·宁波期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D在 $\text{[math]}$ 上，过点D作 $\text{[math]}$ 的垂线，分别交射线 $\text{[math]}$ ，线段 $\text{[math]}$ 于点E，F，连接 $\text{[math]}$ ， $\text{[math]}$ 恰好平分 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长是.

答案解析收藏纠错 + 选题
3. (2023八上·金华期末) 如图，在 $\text{[math]}$ 中，过点B作 $\text{[math]}$ 的角平分线 $\text{[math]}$ 的垂线，垂足为F， $\text{[math]}$ 交 $\text{[math]}$ 于点G，若 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为 .

答案解析收藏纠错 + 选题
4. (2022八上·大连期末) 如图， $\text{[math]}$ 是等边三角形，D是 $\text{[math]}$ 边上一点，在 $\text{[math]}$ 右侧作 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是等边三角形；
2. （2）若D是等边 $\text{[math]}$ 外一点，且与点A都在直线 $\text{[math]}$ 同侧，若 $\text{[math]}$ ，连接 $\text{[math]}$ ，画出图形，探究线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并说明理由．
答案解析收藏纠错 + 选题
5. (2023八上·安顺期末) 如图，在 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线，点 $\text{[math]}$ 是 $\text{[math]}$ 边上一动点，点 $\text{[math]}$ 是 $\text{[math]}$ 上的一个动点．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ 时，求 $\text{[math]}$ 的长；
3. （3）在（2）的条件下，请直接写出 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
6. (2023八上·达州期末) 如图，等腰直角三角形ABC中，∠BAC＝90°，D、E分别为AB、AC边上的点，AD＝AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．
1. （1）求证：△ADC≌△AEB；
2. （2）判断△EGM是什么三角形，并证明你的结论；
3. （3）判断线段BG、AF与FG的数量关系并证明你的结论．
答案解析收藏纠错 + 选题
7. (2022八上·中山期末) 如图， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，点 $\text{[math]}$ 与点 $\text{[math]}$ 关于 $\text{[math]}$ 对称， $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
8. (2023八上·大冶) 如图，在等边△ABC中，点D为边BC上一点，∠ABE＝∠CAD，CF∥BE交AD的延长线于点F.
1. （1）求∠AEB的度数；
2. （2）若BE＝10，AF＝15，求AE的长.
答案解析收藏纠错 + 选题
9. (2023八上·扶沟期末) 已知，在等边三角形 $\text{[math]}$ 中，点O在 $\text{[math]}$ 上，点P在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ .
1. （1）如图1，当点O为 $\text{[math]}$ 的中点时，确定线段 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，请你直接写出结论；
2. （2）如图2，当点O为 $\text{[math]}$ 边上任意一点，确定线段 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，请你写出结论，并说明理由；
3. （3）在等边三角形 $\text{[math]}$ 中，点O在直线 $\text{[math]}$ 上，点P在线段 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ，若 $\text{[math]}$ 的边长为2， $\text{[math]}$ ，求 $\text{[math]}$ 的长.（请画出相应图形，并写出解题过程）
答案解析收藏纠错 + 选题
10. (2023八上·大冶) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 内一点， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 60° B . 72° C . 70° D . 65°

答案解析收藏纠错 + 选题

二、二阶段（中等）

11. (2023八下·杭州期中) 如图，在 ▱ ABCD，点F是BC上的一点，连接AF，AE平分∠FAD，交CD于中点E，连接EF．若∠FAD＝60°，AD＝5，CF＝3，则EF＝．

答案解析收藏纠错 + 选题
12. (2023八下·杭州期中) 如图，正方形ABCD的边长为2，G是对角线BD上一动点，GE⊥CD于点E，GF⊥BC于点F，连结EF．给出四种情况：

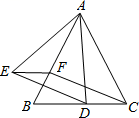
①若G为BD上任意一点，则AG=EF；

②若BG=AB，则∠DAG=22.5°；

③若G为BD的中点，则四边形CEGF是正方形；

④若DG：BG=1：3，则S_△_ADG= $\text{[math]}$

则其中正确的是.

答案解析收藏纠错 + 选题
13. (2023·秀洲模拟) 如图，分别以正方形ABCD的两条边AD、CD为边向外作两个正三角形，即△ADG与△CDF，然后延长GA，FC交于点E，得到一个“镖型”ABCE.已知正方形ABCD的边长为2，则“镖型”ABCE的周长为（）

A . 8+ $\text{[math]}$ B . 4+4 $\text{[math]}$ C . 4+4 $\text{[math]}$ D . 8+4 $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2023八下·杭州月考) 在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 中点，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，连接 $\text{[math]}$ ，在 $\text{[math]}$ 下方有一点 $\text{[math]}$ ，满足 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
15. (2023·深圳模拟) 如图，已知射线BC⊥AB，以AB为斜边作Rt△ABD，延长AD到E，使得AD＝DE，连接BE，BF平分∠CBE交AE于点F．
1. （1）求证：BD＝DF；
2. （2）若AB＝2，以AE为边向下作∠AEG＝45°，交射线BC于点G，求BG的长．
答案解析收藏纠错 + 选题
16. (2023八上·宁波期末) 如图，点A，B，C，D顺次在直线l上， $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为边向下作等边 $\text{[math]}$ ，以 $\text{[math]}$ 为底边向上作等腰 $\text{[math]}$ ，当 $\text{[math]}$ 的长度变化时， $\text{[math]}$ 与 $\text{[math]}$ 的面积差S始终保持不变，则a，b满足（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2023八上·金华期末) 如图，在△ABC中，∠ABC＝2∠ACB，BD为△ABC的角平分线；
1. （1）若AB＝BD，则∠A的度数为 °（直接写出结果）；
2. （2）如图1，若E为线段BC上一点，∠DEC＝∠A；求证：AB＝EC.
3. （3）如图2，若E为线段BD上一点，∠DEC＝∠A，求证：AB＝EC.
答案解析收藏纠错 + 选题
18. (2022八上·招远期末) $\text{[math]}$ 和 $\text{[math]}$ 都是等边三角形，当 $\text{[math]}$ 绕点A旋转到图1的位置时，连接连接 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）请猜想线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间有怎样的数量关系？并加以证明；
2. （2）将 $\text{[math]}$ 绕点A旋转到图2的位置时，其他条件不变，请直接写出线 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，不需要证明．
答案解析收藏纠错 + 选题
19. (2022八上·拱墅月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 的中点， $\text{[math]}$ 、 $\text{[math]}$ 分别为边 $\text{[math]}$ 、 $\text{[math]}$ 上的点，且 $\text{[math]}$ ， $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ，线段 $\text{[math]}$ 的长度 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023八上·华蓥期末) 如图，在等边 $\text{[math]}$ 中，点D，E分别是 $\text{[math]}$ 上的动点，且 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点P.
1. （1）如图1，求证： $\text{[math]}$ ；
2. （2）点M是边 $\text{[math]}$ 的中点，连接 $\text{[math]}$ .
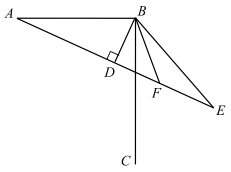
  ①如图2，若点A，P，M三点共线，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是 .
  
  ②若点A，P，M三点不共线，问①中的结论还成立吗？若成立，请给出证明，若不成立，说明理由.
答案解析收藏纠错 + 选题

三、三阶段（较难）

21. (2023八下·武昌期中) 问题提出：一条线段沿某个方向平移一段距离后与原线段构成一个平行四边形.我们可以利用这一性质，将有些条件通过平移集中在一起来解决一些几何问题.

如图①，两条长度相等的线段 $\text{[math]}$ 和 $\text{[math]}$ 相交于O点， $\text{[math]}$ ，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 的夹角为 $\text{[math]}$ ，求线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 满足的数量关系.

分析：考虑将 $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ 集中到同一个三角形中，以便运用三角形的知识寻求三条线段的数量关系：

如图②，作 $\text{[math]}$ 且 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是平行四边形，从而 $\text{[math]}$ ；

由于 $\text{[math]}$ ， $\text{[math]}$ ，所以 $\text{[math]}$ 是等边三角形，故 $\text{[math]}$ ；

通过平行又求得 $\text{[math]}$ .

在 $\text{[math]}$ 中，研究三条线段的大小关系就可以了.
1. （1）如图②，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 的长；
2. （2）问题解决：如图③，矩形 $\text{[math]}$ 中，E、F分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的点，满足 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）拓展应用：如图④， $\text{[math]}$ 中， $\text{[math]}$ ， D、E分别在 $\text{[math]}$ 、 $\text{[math]}$ 上， $\text{[math]}$ 、 $\text{[math]}$ 交于点O， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .
答案解析收藏纠错 + 选题
22. (2023·江西模拟) 对于一个四边形给出如下定义：一组对角为 $\text{[math]}$ ，一组邻边相等的四边形称为“六零”四边形．
1. （1）图1是一个“六零”四边形，其中 $\text{[math]}$ ， $\text{[math]}$ ．
  ①猜想 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是 ▲ ；
  ②证明你的猜想．
2. （2）图2是一个“六零”四边形，其中 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
  ① $\text{[math]}$ 是三角形；
  ②若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （用含m，n的代数式表示）．
3. （3）在（2）的条件下，如图3，延长 $\text{[math]}$ 到点F，使得 $\text{[math]}$ ，连接DF．求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
23. (2023·四川模拟) 如图，在 $\text{[math]}$ 中，P为平面内的一点，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是（）

A . $\text{[math]}$ B . 36 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
24. (2023八上·武义期末) 如图，在平面直角坐标系中，点A在y轴正半轴上， $\text{[math]}$ .在第一象限内作等腰 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .点D为x轴正半轴上的动点，连接AD，将线段AD绕点A逆时针旋转a度，得到线段AE，连接EC并延长交x轴于点F.
1. （1）如图1，当 $\text{[math]}$ 时，线段OF与CF的数量关系是；
2. （2）如图2，当 $\text{[math]}$ 时，（1）中的结论是否还成立？若成立，请给予证明；若不成立，请说明理由；
3. （3）若 $\text{[math]}$ ，
  ①求点F的坐标；
  ②过点E作 $\text{[math]}$ 轴，垂足为P，当 $\text{[math]}$ 是等腰三角形时，求P点的坐标.
答案解析收藏纠错 + 选题
25. (2023八上·镇海区期末) 如图，在边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 中，过 $\text{[math]}$ 中点E作正 $\text{[math]}$ ，过点F的直线分别交边 $\text{[math]}$ 、 $\text{[math]}$ 于点G、H、已知点M、N分别是线段 $\text{[math]}$ 、 $\text{[math]}$ 的动点，且 $\text{[math]}$ 是等边三角形.
1. （1）判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由.
2. （2）当点N在线段 $\text{[math]}$ 上时
  ①求证： $\text{[math]}$
  ②试判断 $\text{[math]}$ 的结果是否变化？若变化，请说明理由；若不变，请求出这个值.
3. （3）设 $\text{[math]}$ ，点A关于 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，若点 $\text{[math]}$ 落在 $\text{[math]}$ 的内部，请直接写出 $\text{[math]}$ 的范围.
答案解析收藏纠错 + 选题
26. (2023八上·鄞州期末) 如图1，在Rt△ABC中，∠BAC＝90°，AB＝4，以AB为边在AB上方作等边△ABD，以BC为边在BC右侧作等边△CBE，连结DE.
1. （1）当AC＝5时，求BE的长.
2. （2）求证：BD⊥DE.
3. （3）如图2，点C′与点C关于直线AD对称，连结C′E.
  ①求C′E的长.
  
  ②连结C′D，当△C′DE是以C′E为腰的等腰三角形时，写出所有满足条件的AC长：　 .（直接写出答案）
答案解析收藏纠错 + 选题
27. (2023八上·鄞州期末) 如图，在△ABC中，E是AB中点，F是AC上一动点，连结EF，将△AEF沿直线EF折叠得△DEF．
1. （1）如图①，若∠B=45°，且点D恰好落在线段BC上，求证：点F为线段AC的中点；
2. （2）如图②，若△ABC为等边三角形，且边长为4，当点D落在线段CE上时，求AF的长度；
3. （3）如图③，若△ABC为直角三角形，∠BAC=90°，AC=8．连结AD、BD、CD，若△ACD与△BDC面积相等，且CD=4，求△ABC的面积．
答案解析收藏纠错 + 选题
28. (2023八上·大冶) 如图，在等边 $\text{[math]}$ 中，D为 $\text{[math]}$ 上一点， $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）如图1，若点E在 $\text{[math]}$ 边上，求证： $\text{[math]}$ ；
2. （2）如图2，若点E在 $\text{[math]}$ 内，连接CE，F为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
29. (2022八上·义乌期末) 如图，已知 $\text{[math]}$ 为等腰直角三角形，且面积为4.点D是 $\text{[math]}$ 的中点，点F是直线 $\text{[math]}$ 上一动点，连结 $\text{[math]}$ .
1. （1）求线段 $\text{[math]}$ 的长；
2. （2）当点E在射线 $\text{[math]}$ 上，且 $\text{[math]}$ 时，连结 $\text{[math]}$ ，若 $\text{[math]}$ ，试判断 $\text{[math]}$ 是否为等腰三角形，并说明理由；
3. （3）直线 $\text{[math]}$ 上是否存在点F（F不与 $\text{[math]}$ 重合），使 $\text{[math]}$ 的其中两边之比为 $\text{[math]}$ ？若存在，求出 $\text{[math]}$ 的长；若不存在，请说明理由.
答案解析收藏纠错 + 选题
30. (2022八上·临海期末) 如图1，已知 $\text{[math]}$ ，定点P在射线 $\text{[math]}$ 上，动点B在射线 $\text{[math]}$ 上，作凸四边形 $\text{[math]}$ ，使 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）如图1，当 $\text{[math]}$ 为锐角时.
  ①若 $\text{[math]}$ ，试用含 $\text{[math]}$ 的式子表示 $\text{[math]}$ ；
  ②过点C作 $\text{[math]}$ 于点H，求证： $\text{[math]}$ .
2. （2）如图2，当点B运动到 $\text{[math]}$ 时，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点K，试用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并说明理由；
3. （3）若点B关于直线 $\text{[math]}$ 的对称点为点D，连接 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 为等腰直角三角形时，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题