人教版初中数学几何辅助线进阶训练——菱形的辅助线（不含相似）

更新时间：2023-05-11 浏览次数：68 类型：复习试卷

一、阶段一（较易）

1. (2023八下·青秀月考) 如图，菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 中点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 是矩形.
2. （2）求 $\text{[math]}$ 的度数.
3. （3）求菱形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
2. (2023·广西模拟) 在 $\text{[math]}$ 中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作 $\text{[math]}$ 交BE的延长线于点F.
1. （1）求证： $\text{[math]}$ ；
2. （2）证明：四边形ADCF是菱形：
3. （3）若AC＝3，AB＝4，求菱形ADCF的面积.
答案解析收藏纠错 + 选题
3. (2023·滁州模拟) 如图，四边形 $\text{[math]}$ 为菱形，点E是 $\text{[math]}$ 的中点，点F，H是对角线 $\text{[math]}$ 上两点，且 $\text{[math]}$ ，点G在边 $\text{[math]}$ 上．若四边形 $\text{[math]}$ 是矩形，则菱形 $\text{[math]}$ 的周长为．

答案解析收藏纠错 + 选题
4. (2023·南岗模拟) 如图1，平行四边形 $\text{[math]}$ 中，点E、点F分别是 $\text{[math]}$ 上的点，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形．
2. （2）如图2，当点E是AD中点时， $\text{[math]}$ 与 $\text{[math]}$ 交于点O，连接 $\text{[math]}$ ，请直接写出图2中四个三角形，使写出的每个三角形的面积等于 $\text{[math]}$ 面积3倍．
答案解析收藏纠错 + 选题
5. (2022·青县模拟) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，点F为 $\text{[math]}$ 的中点， $\text{[math]}$ 于E，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022九上·章丘期中) 如图，在矩形ABCD中，AB＝24，BC＝12，点E在边AB上，点F在边CD上，点G、H在对角线AC上，若四边形EGFH是菱形．则AE的长是（）

A . 15 B . 20 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022九上·成都月考) 如图，四边形 $\text{[math]}$ 是平行四边形，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点O， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
8. (2023·雁塔模拟) 如图，在菱形 $\text{[math]}$ 中，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 交对角线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
9. (2022八下·泉港期末) 如图，菱形ABCD中， $\text{[math]}$ ， AD的垂直平分线交对角线BD于点P，垂足为N，连结CP，则∠BPC＝度．

答案解析收藏纠错 + 选题
10. (2023八下·莱芜期中) 如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE=BF，连接AE，CF．
1. （1）求证：△ADE≌△CBF；
2. （2）试连接AF，CE．当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．
答案解析收藏纠错 + 选题

二、阶段二（中等）

11. (2022九上·岳麓月考) 如图所示，在菱形ABCD中，AB＝6，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．当点E、F在BC、CD上滑动时，△CEF的面积最大值是（）

A . 4 $\text{[math]}$ B . $\text{[math]}$ C . 3 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2022九上·新城月考) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，点 $\text{[math]}$ 、 $\text{[math]}$ 在对角线 $\text{[math]}$ 上，若四边形 $\text{[math]}$ 是菱形．则 $\text{[math]}$ 的长是（）

A . 15 B . 20 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2022八下·曲阳期末) 如图， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上，连接 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是矩形；
2. （2）过 $\text{[math]}$ 作 $\text{[math]}$ ，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ ，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，得到四边形 $\text{[math]}$ ，此时，求证四边形 $\text{[math]}$ 是菱形．
答案解析收藏纠错 + 选题
14. (2022八下·黄山期末) 如图，菱形ABCD的边长是4，∠A=60°，点G为AB的中点，以BG为边作菱形BEFG，其中点E在CB的延长线上，点P为FD的中点，连接PB．则PB=．

答案解析收藏纠错 + 选题
15. (2022八下·成都期末) 如图，菱形ABCD的对角线AC与BD交于点O，点E是AD边上一点，且 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则AE的长是．

答案解析收藏纠错 + 选题
16. (2022·海曙模拟) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ， $\text{[math]}$ ，下列结论：① $\text{[math]}$ ，② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，其中正确结论的个数共有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
17. (2022·临安模拟) ▱ ABCD 中， ∠BAD的平分线交直线 BC 于点 E，线 DC于点 F
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2021九上·罗湖期中) （问题发现）数学小组成员小明做作业时遇到以下问题：

图1 图2 图3
1. （1）若四边形 $\text{[math]}$ 是菱形， $\text{[math]}$ ，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上一动点，以 $\text{[math]}$ 为边向右侧作等边 $\text{[math]}$ ，如图1，当点E在菱形 $\text{[math]}$ 内部或边上时，连接 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 有怎样的数量关系？请直接写出你的猜想；
2. （2）（类比探究）数学小组对该问题进行进一步探究：
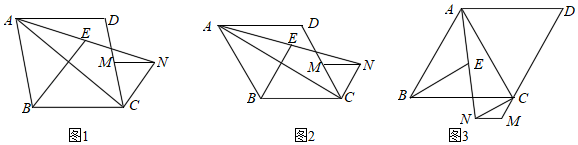
  若四边形 $\text{[math]}$ 是正方形，点P是射线 $\text{[math]}$ 上一动点，以 $\text{[math]}$ 为直角边在 $\text{[math]}$ 边的右侧作等腰 $\text{[math]}$ ，其中 $\text{[math]}$ .
  
  ①如图2，当点 $\text{[math]}$ 在对角线 $\text{[math]}$ 上时，小组发现点 $\text{[math]}$ 恰好在射线 $\text{[math]}$ 上，求 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系（过程只用说明点 $\text{[math]}$ 在线段 $\text{[math]}$ 上的情况即可）；
  
  ②如图3，当P是对角线 $\text{[math]}$ 的延长线上一动点时，小组发现点 $\text{[math]}$ 恰好在射线 $\text{[math]}$ 上，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
19. (2021九上·鹤壁月考) 在菱形ABCD中，∠ABC=60°，E是对角线AC上任意一点，F是线段BC延长线上一点，且CF=AE，连接BE，EF。
1. （1）如图1，当E是线段AC的中点时，BE和EF的数量关系是；
2. （2）如图2，当点E不是线段AC的中点，其它条件不变时，请你判断(1)中的结论是否成立？若成立，请给予证明：若不成立，请说明理由；
3. （3）如图3，当点E是线段AC延长线上的任意一点，其它条件不变时，(1)中的结论是否成立？若成立，请给予证明；若不成立，请说明理由。
答案解析收藏纠错 + 选题
20. (2021八下·乐山期末) 如图，菱形ABCD中，AB=4，∠ABC=120°，过对角线AC延长线上的一点P分别作AD、DC延长线的垂线，垂足分别为E、F，则PE-PF= 。

答案解析收藏纠错 + 选题

三、阶段三（较难）

21. (2023·西安模拟) 如图，在平面直角坐标系中，菱形 $\text{[math]}$ 的对角线 $\text{[math]}$ 上有P，Q两个动点，且 $\text{[math]}$ ，已知点 $\text{[math]}$ ，当 $\text{[math]}$ 周长最小时，点P的坐标为.

答案解析收藏纠错 + 选题
22. (2023九上·西安期末) 在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， P是直线 $\text{[math]}$ 上一动点，以 $\text{[math]}$ 为边向右侧作等边 $\text{[math]}$ （A，P，E按逆时针排列），点E的位置随点P的位置变化而变化.
1. （1）如图1，当点P在线段 $\text{[math]}$ 上，且点E在菱形 $\text{[math]}$ 内部或边上时，连接 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是， $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是；
2. （2）如图2，当点P在线段 $\text{[math]}$ 上，且点E在菱形 $\text{[math]}$ 外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；
3. （3）当点P在直线 $\text{[math]}$ 上时，其他条件不变，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
23. (2022九上·秦都开学考) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别为线段 $\text{[math]}$ 、 $\text{[math]}$ 上的两点．且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$
1. （1）证明： $\text{[math]}$ ≌ $\text{[math]}$ ；
2. （2）求 $\text{[math]}$ 的度数；
3. （3）证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2022九上·温州开学考) 菱形 $\text{[math]}$ 的边长为 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 中点， $\text{[math]}$ 是线段 $\text{[math]}$ 上任一点，连接 $\text{[math]}$ ，作 $\text{[math]}$ ，边 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ．

小南和小浦观察以上问题时，猜想 $\text{[math]}$ ，老师引导他们用“从特殊到一般”的思想方法去尝试研究．
1. （1）【特例发现】
  小南发现：当点 $\text{[math]}$ 与点重合时， $\text{[math]}$ 与 $\text{[math]}$ 的长度相等，为；
2. （2）【探究证明】
  小浦认为当 $\text{[math]}$ 在线段 $\text{[math]}$ 上时，均有“ $\text{[math]}$ ”，请帮助完成证明．
3. （3）【拓展运用】
  ①连结 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ 为定值．
  ②当 $\text{[math]}$ 时， $\text{[math]}$ ▲ ．
答案解析收藏纠错 + 选题
25. (2022八下·临海期末) 小明同学学习了菱形的知识后，结合之前学习的赵爽弦图，编了一个菱形版“赵爽弦图” $\text{[math]}$ 如图，菱形 $\text{[math]}$ 中， $\text{[math]}$ ，四边形 $\text{[math]}$ 是矩形，若 $\text{[math]}$ ，则矩形 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
26. (2022八下·嵊州期末) 已知，菱形ABCD（∠C＜90°）的对角线长分别为6和8，点E在边BC上，BE＝1，若点F在直线AB上，且AE＝DF，则BF的长为.

答案解析收藏纠错 + 选题
27. (2022八下·仙居期中) 如图，四边形ABCD是菱形，点M在CD边上，点N在菱形ABCD外部，且满足MN∥AD，CM＝MN，连接AN，CN，取AN的中点E，连接BE，AC.
1. （1）探究BE与AC的关系；
2. （2）若∠ABC＝120°，探究线段BE、AD、CM所满足的等量关系；
3. （3）若∠ABC＝60°，M在DC的延长线上时，其余条件不变，CM＝1，AD＝3，请求出BE的长度.
答案解析收藏纠错 + 选题
28. (2021九上·成都月考) 如图，菱形ABCD中，AB＝12，∠BAD＝60°，E为线段BC的中点.若点P是线段AB上的一动点，Q为线段AD上一动点，则 $\text{[math]}$ PQE的周长的最小值是.

答案解析收藏纠错 + 选题
29. (2021八下·大东期末) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， E是对角线 $\text{[math]}$ 上一点，F是线段 $\text{[math]}$ 延长线上一点且 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）如图，若E是线段 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，其他条件不变，直接写出线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系；
2. （2）如图，若E是线段 $\text{[math]}$ 上任意一点，连接 $\text{[math]}$ ，其他条件不变，猜想线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是什么？并证明你的猜想；
3. （3）如图，若E是线段 $\text{[math]}$ 延长线上一点，其他条件不变，且 $\text{[math]}$ ，菱形 $\text{[math]}$ 的周长为 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
30. (2021八下·和平期末) 如图，在▱ABCD中，对角线BD的垂直平分线分别与AD，BC，BD相交于点E，F，O．
1. （1）求证：四边形BEDF是菱形；
2. （2）在▱ABCD中，若AB＝2.5，AD＝4，有两动点P，Q分别从B，D两点同时出发，沿△BAE和△DFC各边运动一周，即点P自B→A→E→B停止，点Q自D→F→C→D停止，点P运动的路程是x，点Q运动的路程是y，当四边形BPDQ是平行四边形时，则请直接写出x+y的值为．
答案解析收藏纠错 + 选题