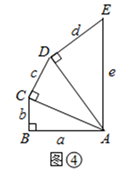
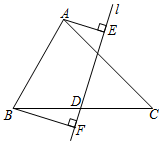


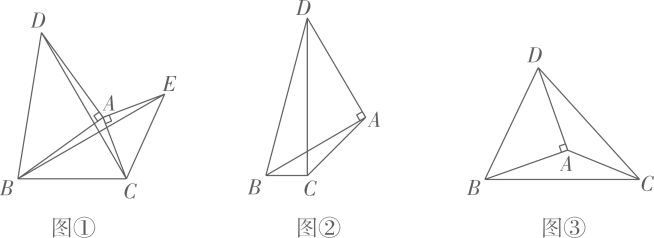
[感知]如图①,以△ABC的边AB、AC为直角边,A为直角顶点,向外作等腰直角△ABD和等腰直角△ACE,连结BE、CD,易知△ADC≌△ABE.(不要求证明)
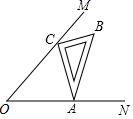
[探究]如图②,在△ABC中,已知∠ACB=135°,∠BAD=90°,BC=1,AC=2,AB=AD,求CD的长.
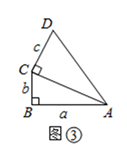
[应用]如图③,在△ABC中,BC=2,AC=1.以△ABC的边AB为直角边,A为直角顶点,向外作等腰直角△ABD,则线段CD长度的最大值是 ▲
已知点N(3,0),A(1,0), ,
.
②点D(a,0),若点C为线段OD的“二分点”,求a的取值范围;
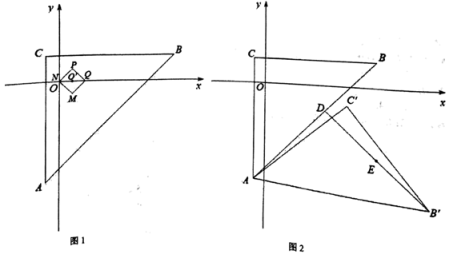
①原点O与线段BC的“近距离”为;
②如图1,正方形PQMN在△ABC内,中心O’坐标为(m,0),若正方形PQMN与△ABC的边界的“近距离”为1,则m的取值范围为;
已知A(-4,0),B(0,4),C(4,0),D(0,-4),
① 当r = 1时,求 ⊙O与正方形ABCD的“近距离”d(⊙O,正方形ABCD);
② 若d(⊙O,正方形ABCD)=1,则r = ▲ .
 ①在点O视角下,则线段
①在点O视角下,则线段 的“宽度
”为;
②若 半径为1.5,在点A视角下,
的“宽度
”为;
若随着点C位置的变化,使得在所有点K的视角下,线段 的“宽度”均满足
,直接写出m的取值范围.
|
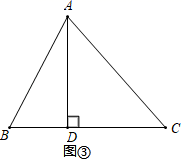
数学活动课上,老师提出如下问题: 如图①,在四边形ABCD中,AB⊥BC,DC⊥BC,AB=2,DC=4,BC=8,点P为BC边上的动点,求当BP的值是多少时,AP+DP有最小值,最小值是多少. 小丽和小明对老师提出的问题进行了合作探究: 小丽:设BP=x,则CP=8﹣x,根据勾股定理,可得AP+DP= 小明:利用轴对称作图,如图②,作点A关于直线BC的对称点A′,连接A′D,与BC交于点P,根据两点之间线段最短,将求AP+DP的最小值转化为求线段A'D的长. 由△A′BP∽△DCP,得 所以BP= 过点A′作A′H⊥DC,交DC的延长线于点H,再由勾股定理,可得A′D= 所以当BP= |
任务:
在平面直角坐标系 中,
的半径为
,若
平移
个单位后,使某图形上所有点在
内或
上,则称
的最小值为
对该图形的“最近覆盖距离”.例如,如图①,
,则
对线段
的“最近覆盖距离”为
.

(概念理解)
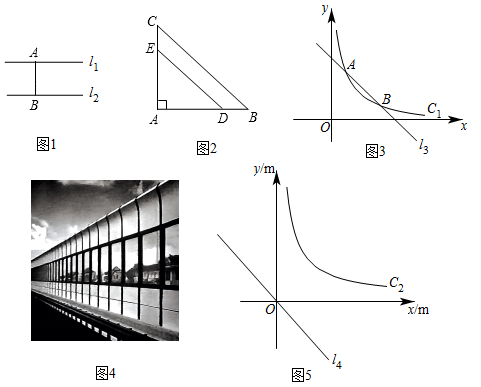
例如,如图1, , 线段
的长度称为点A与直线
之间的距离,当
时,线段
的长度也是
与
之间的距离.
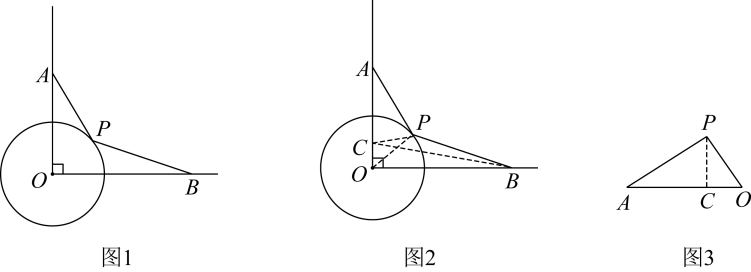
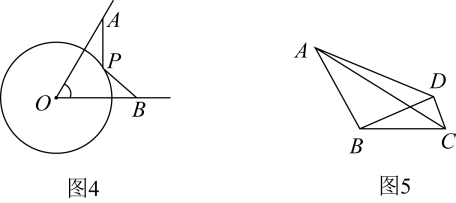
【问题呈现】如图1,∠AOB=90°, OA=4,OB=5,点P在半径为2的⊙O上,求的最小值.
【问题解决】小明是这样做的:如图2,在OA上取一点C使得OC=1,这样可得 , 又因为∠COP=∠POA,所以可得△COP ∽△POA,所以
, 得
所以
.
又因为 , 所以
最小值为 ▲ .
【思路点拨】小明通过构造相似形(图3),将转化成CP,再利用“两点之间线段”最短”求出CP+ BP的最小值.
【尝试应用】如图4,∠AOB=60°, OA=10,OB=9,点P是半径为6的⊙O上一动点,求的最小值.
【能力提升】如图5,∠ABC=120°, BA= BC=8,点D为平面内一点且BD= 3CD,连接AD,则△ABD面积的最大值为 ▲ .
(类比探究)为了解决这个实际问题,我们首先探究下面的数学问题.
探究:如图②,在 中,
.若
,
,
,则
与
之有什么数量关系?
解:在 中,
,
,即
.
,
,
,
,
.
.
,
,
均大于
,
与
之间的数量关系是
.
解:
,
,
,
.
,
,
,
,
,
.
将上面三式相加得, ,
.
.
.
,
,
,
均大于
,
与
之间有这样的数量关系:
.