 B .
B . 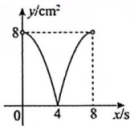 C .
C .  D .
D . 


 B .
B .  C .
C .  D .
D . 
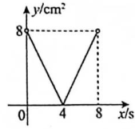
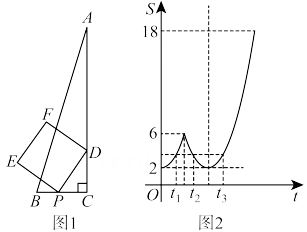
①当点P移动到点A时,点Q移动到点C ②正方形边长为6cm ③当AP=AQ时,△PAQ面积达到最大值④线段EF所在的直线对应的函数关系式为y=−3x+18



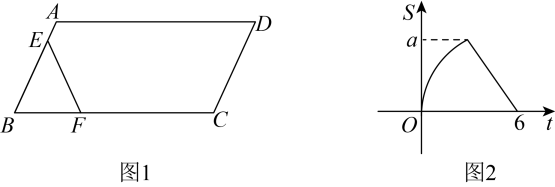

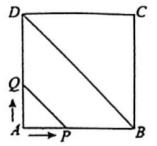
设抛物线的顶点为
, 当点
在
上时,求
的值;
当点
在抛物线上时,求
的值;
当抛物线与正方形
有两个交点时,直接写出
的取值范围.
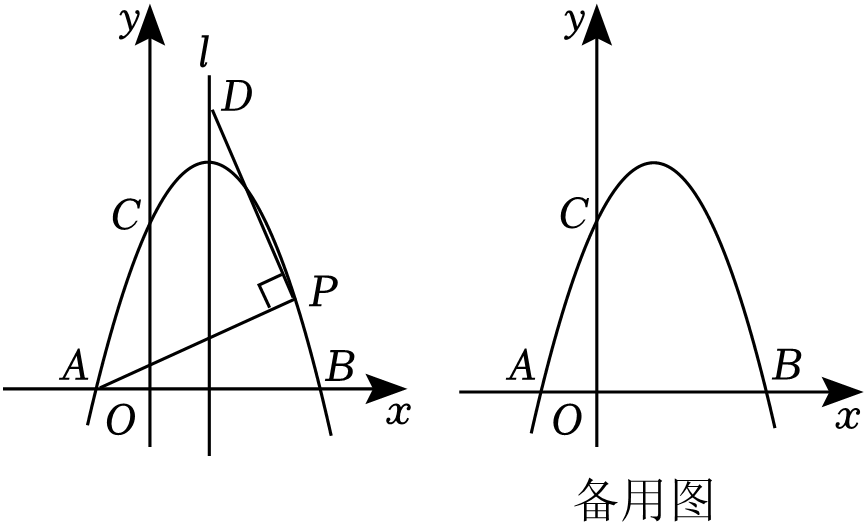
①求d关于m的函数解析式;
②根据d的不同取值,试探索点P的个数情况.
例题:求多项式x2﹣4x+5的最小值.
解:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,所以(x﹣2)2+1≥1.
当x=2时,(x﹣2)2+1=1.因此(x﹣2)2+1有最小值,最小值为1,即x2﹣4x+5的最小值为1.
通过阅读,理解材料的解题思路,请解决以下问题:

已知代数式A=x2+10x+20,则A的最小值为 ;
张大爷家有甲、乙两块长方形菜地,已知甲菜地的两边长分别是(3a+2)米、(2a+5)米,乙菜地的两边长分别是5a米、(a+5)米,试比较这两块菜地的面积S甲和S乙的大小,并说明理由;
如图,△ABC中,∠C=90°,AC=5cm , BC=10cm , 点M、N分别是线段AC和BC上的动点,点M从A点出发以1cm/s的速度向C点运动;同时点N从C点出发以2cm/s的速度向B点运动,当其中一点到达终点时,两点同时停止运动,设运动的时间为t , 则当t的值为多少时,△MCN的面积最大,最大值为多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中, ▲
根据如表数据,在图
所示的平面直角坐标系中,通过描点画出了函数图象的一部分,请画出该函数图象的另一部分
观察图象,写出该函数的一条性质;