备考2024年中考数学探究性训练专题14 反比例函数

更新时间：2024-03-24 浏览次数：22 类型：二轮复习

一、选择题

1. (2023八下·靖江期末) 探究函数 $\text{[math]}$ 的图像发现，可以由 $\text{[math]}$ 的图像先向右平移2个单位，再向上平移3个单位得到．根据以上信息判断，下列直线中与函数 $\text{[math]}$ 的图像没有公共点的是（）

A . 经过点 $\text{[math]}$ 且平行于x轴的直线 B . 经过点 $\text{[math]}$ 且平行于x轴的直线 C . 经过点 $\text{[math]}$ 且平行于y轴的直线 D . 经过点 $\text{[math]}$ 且平行于y轴的直线

答案解析收藏纠错 + 选题
2. (2020·蠡县模拟) 小明使用电脑软件探究函数 $\text{[math]}$ 的图象，他输入了一组a，b的值，得到了下面的函数图象，由学习函数的经验，可以推断出小明输入的a，b的值满足（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020八下·越城期末) 小明使用图形计算器探究函数y＝ $\text{[math]}$ 的图象，他输入了一组a，b的值，得到了下面的函数图象，由学习函数的经验，可以推断出小明输入的a，b的值满足（　　）

A . a＞0，b＞0 B . a＞0，b＜0 C . a＜0，b＞0 D . a＜0，b＜0

答案解析收藏纠错 + 选题
4. (2018·江西) 在平面直角坐标系中，分别过点A（m，0），B（m+2，0）作x轴的垂线l₁和l₂ ，探究直线l₁ ，直线l₂与双曲线y= $\text{[math]}$ 的关系，下列结论错误的是（）

A . 两直线中总有一条与双曲线相交 B . 当m=1时，两直线与双曲线的交点到原点的距离相等 C . 当﹣2＜m＜0时，两直线与双曲线的交点在y轴两侧 D . 当两直线与双曲线都有交点时，这两交点的最短距离是2

答案解析收藏纠错 + 选题
5. 某学习小组，在探究1+ $\text{[math]}$ 的性质时，得到了如下数据：
x
1
10
100
1000
10000
…
1+ $\text{[math]}$
3
1.2
1.02
1.002
1.0002
…
根据表格中的数据，做出了四个推测：
①1+ $\text{[math]}$ （x＞0）的值随着x的增大而减小；
②1+ $\text{[math]}$ （x＞0）的值有可能等于1；
③1+ $\text{[math]}$ （x＞0）的值随着x的增大越来越接近于1；
④1+ $\text{[math]}$ （x＞0）的值最大值是3．则推测正确的有（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

6. (2023·吴兴模拟) 如图1，点 $\text{[math]}$ 是反比例函数 $\text{[math]}$ 的图象上一点，连接$OA$，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，已知点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，连接 $\text{[math]}$ ，小明通过对 $\text{[math]}$ 和 $\text{[math]}$ 的面积与 $\text{[math]}$ 的关系展开探究，发现 $\text{[math]}$ 的值为；如图2，延长 $\text{[math]}$ 交 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，依此进行下去.记 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
7. (2021·燕山模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，已知直线 $\text{[math]}$ ，双曲线 $\text{[math]}$ ，在l上取一点 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线交双曲线于点 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线交l于点 $\text{[math]}$ ，请继续操作并探究：过 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线交双曲线于点 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线交l于点 $\text{[math]}$ ，…，这样依次得到l上的点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，…， $\text{[math]}$ ，…，记点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ；若要将上述操作无限次地进行下去，则 $\text{[math]}$ 不能取的值是．

答案解析收藏纠错 + 选题

三、理论探究题

8. (2023八下·广陵期末) 对于某些函数，由自变量的大小关系确定函数值的大小关系，不仅可以利用函数的图象判断，也可以用代数的方法判断，这是“数形结合”思想的典型应用．
1. （1）已知一次函数 $\text{[math]}$ 的图象上的两点 $\text{[math]}$ ，如何用代数的方法判断 $\text{[math]}$ 的大小关系呢？由点 $\text{[math]}$ 都在函数图象上，得 $\text{[math]}$ ， $\text{[math]}$ ，再将 $\text{[math]}$ 作差，按照该思路写出判断过程；
2. （2）已知反比例函数 $\text{[math]}$ 的图象上的两点 $\text{[math]}$ ，仿照（1）中的思路写出 $\text{[math]}$ 的大小关系的判断过程．
答案解析收藏纠错 + 选题

四、数形结合探究题

9. (2023·深圳模拟) 某数学学习小组在研究函数 $\text{[math]}$ 时，对函数的图象和性质进行了探究．
探究过程如下：
1. （1） x与y的几组对应值如表：
  x
  …
  ﹣2
  ﹣1
  0
  1
  $\text{[math]}$
  $\text{[math]}$
  3
  4
  5
  6
  …
  y
  …
  $\text{[math]}$
  m
  0
  ﹣1
  n
  5
  3
  2
  $\text{[math]}$
  $\text{[math]}$
  …
  其中 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）在平面直角坐标系 $\text{[math]}$ 中，描出上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；
3. （3）观察图像，我们可以认为函数 $\text{[math]}$ 的图像可由函数 $\text{[math]}$ 的图像向右平移个单位，再向上平移个单位得到；
4. （4）根据函数图象，当 $\text{[math]}$ 时，自变量x的取值范围为．
答案解析收藏纠错 + 选题

10. (2020八下·襄汾期末) 有这样一个问题：探究函数y= $\text{[math]}$ 的图象与性质．小慧根据学习函数的经验，对函数y= $\text{[math]}$ 的图象与性质进行了探究．下面是小慧的探究过程，请补充完成：

（1）函数y= $\text{[math]}$ 的自变量x的取值范围是；

（2）列出y与x的几组对应值．请直接写出m的值，m=；

x	…	-3	-2	0	1	1.5	2.5	m	4	6	7	…
y	…	2.4	2.5	3	4	6	-2	0	1	1.5	1.6	…

（3）请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，写出该函数的两条性质：
①；

②．

答案解析收藏纠错 + 选题

11. (2020九上·重庆开学考) 启航同学根据学习函数的经验，对函数 $\text{[math]}$ 的图象与性质进行了探究.下面是他的探究过程，请补充完成：

（1）函数 $\text{[math]}$ 的自变量x 的取值范围是；

（2）列表，找出y 与x 的几组对应值，列表如下：

x	…	-2	-1	0	$\text{[math]}$	$\text{[math]}$	2	3	..
y	…	a	$\text{[math]}$	1	2	2	1	$\text{[math]}$	…

其中， a=；

（3）在平面直角坐标系xOy 中，描出以上表中各对对应值为坐标的点，并画出该函数的图象并写出该函数的一条性质：

答案解析收藏纠错 + 选题

12. (2020·荆州) 九年级某数学兴趣小组在学习了反比例函数的图象和性质后，进一步研究了函数 $\text{[math]}$ 的图像与性质，其探究过程如下：
1. （1）绘制函数图象，如图1
  ①列表；下表是x与y的几组对应值，其中 m= ；
  
  ②描点：根据表中各组对应值(x，y)在平面直角坐标系中描出了各点；
  
  ③连线：用平滑的曲线顺次连接各点，画出了部分图像，请你把图像补充完整；
2. （2）通过观察图1，写出该函数的两条性质：①；②；
3. （3） ①观察发现：如图2，若直线y=2交函数 $\text{[math]}$ 的图像于A，B两点，连接OA，过点B作BC//OA交x轴于点C，则S_OABC=；
  ②探究思考：将①的直线y=2改为直线y=a(a>0)，其他条件不变，则S_OABC=；
  
  ③类比猜想：若直线y=a(a>0)交函数 $\text{[math]}$ 的图像于A，B两点，连接OA，过点B作BC//OA交x轴于C，则 S_OABC= ；
答案解析收藏纠错 + 选题
13. (2022八下·临汾期末) 综合与探究
如图，已知， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， D为B点关于 $\text{[math]}$ 的对称点，反比例函数 $\text{[math]}$ 的图象经过D点．
1. （1）证明四边形 $\text{[math]}$ 为菱形；
2. （2）求此反比例函数的解析式；
3. （3）已知在 $\text{[math]}$ 的图象（ $\text{[math]}$ ）上有一点N，y轴正半轴上有一点M，且四边形 $\text{[math]}$ 是平行四边形，求M点的坐标．
答案解析收藏纠错 + 选题
14. (2024九上·祁阳期末) 在平面直角坐标系中，对于不在坐标轴上的任意点 $\text{[math]}$ ，我们把点B $\text{[math]}$ 称为点A的“倒数点”．
1. （1）写出平面直角坐标系中第三象限内“倒数点”是本身的点的坐标；
2. （2）点P是反比例函数 $\text{[math]}$ 图象上的一点，求出点P的“倒数点”Q满足的函数表达式；
3. （3）如图，矩形 $\text{[math]}$ 的顶点 $\text{[math]}$ ，顶点E在y轴上，函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 交于点A ．若点B点A的“倒数点”，且点B在矩形 $\text{[math]}$ 的一边上，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
15. 背景：点A在反比例函数y= $\text{[math]}$ （k>0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，分别在射线AC，BO上取点D，E，使得四边形ABED为正方形.如图1，点A在第一象限内，当AC=4时，小李测得CD=3.
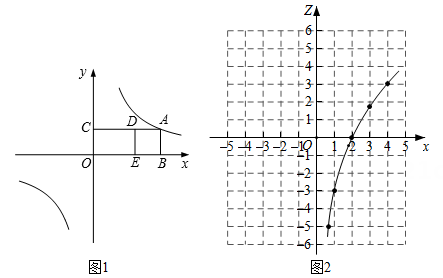
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系.请帮助小李解决下列问题.
1. （1）求k的值.
2. （2）设点A，D的横坐标分别为x，z，将z关于x的函数称为“Z函数”.如图2，小李画出了x>0时“Z函数”的图象.
  ①求这个“Z函数”的表达式.
  ②补画x<0时“Z函数”的图象，并写出这个函数的性质（两条即可）.
  ③过点（3，2）作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标.
答案解析收藏纠错 + 选题
16. (2021八下·江干期末) 阅读材料：
已知：一次函数y＝﹣x+b与反比例函数y＝ $\text{[math]}$ （x＞0），当两个函数的图象有交点时，求b的取值范围.
1. （1）方方给出了下列解答：
  ﹣x+b＝ $\text{[math]}$
  
  x²﹣bx+4＝0
  
  ∵两个函数有交点
  
  ∴△＝b²﹣16≥0
  
  但是方方遇到了困难：利用已学的知识无法解b²﹣16≥0这个不等式；
  
  此时，圆圆提供了另一种解题思路；
  
  第1步：先求出两个函数图象只有一个交点时，b＝ ▲ ；
  
  第2步：画出只有一个交点时两函数的图象（请帮圆圆在直角坐标系中画出图象）；
  
  第3步：通过平移y＝﹣x+b的图象，观察得出两个函数的图象有交点时b的取值范围是 ▲ .
  
  应用：
  
  如图，Rt△ABC中，∠C＝90°，BC的长为x，AC的长为y，且S_△ABC＝12.
2. （2）求y关于x的函数表达式；
3. （3）设x+y＝m，求m的取值范围.
答案解析收藏纠错 + 选题
17. (2023八下·洪洞期末) 综合与探究：如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，分别连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求这个反比例函数的表达式；
2. （2）已知点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
3. （3）在平面内是否存在一点P，使以点O，B，A，P为顶点的四边形为平行四边形？若存在，请直接写出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
18. 如图，矩形ABCO在平面直角坐标系中，点A(-5，0)，C(0，6)，反比例函数图象 L₁ 对应的函数表达式为 $\text{[math]}$ 反比例函数图象 L₂ 对应的函数表达式为 $\text{[math]}$ 把矩形 ABCO内部(不含边界)横、纵坐标均为整数的点称为“整点”.
1. （1）若 k=-12，则L₂和L₁ 之间(不含边界)有个“整点”.
2. （2）若L₂ 和L₁之间(不含边界)有4个“整点”，求k的取值范围.
答案解析收藏纠错 + 选题
19. 阅读理解：
在平面直角坐标系中，点M的坐标为(x₁ ， y₁)，点N的坐标为(x₂ ， y₂)，且x₁≠x₂ ， y₁≠y₂ ，若M，N为某矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为M，N的“相关矩形”．如图中的矩形为点M，N的“相关矩形”。
1. （1）已知点A的坐标为(2，0)．
  ①若点B的坐标为(4，4)，则点A，B的“相关矩形”的周长为；
  ②若点C在直线x=4上，且点A，C的“相关矩形”为正方形，求直线AC的表达式．
2. （2）已知点P的坐标为(3，-4)，点Q的坐标为(6，-2)，若使函数y= $\text{[math]}$ 的图象与点P，Q的“相关矩形”有两个公共点，直接写出k的取值范围．
答案解析收藏纠错 + 选题
20. (2023八下·高邮期末) 如图，点P是y轴正半轴上的一个动点，过点P作y轴的垂线，与反比例函数 $\text{[math]}$ 的图象交于点A．把直线l上方的反比例函数图象沿着直线l翻折，其它部分保持不变，所形成的新图象称为“ $\text{[math]}$ 的l镜像”．
1. （1）当 $\text{[math]}$ 时；
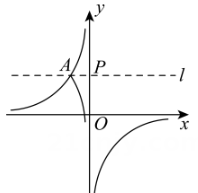
  ①点 $\text{[math]}$ “ $\text{[math]}$ 的l镜像”；（填“在”或“不在”）
  ②“ $\text{[math]}$ 的l镜像”与x轴交点坐标是；
2. （2）过y轴上的点 $\text{[math]}$ 作y轴垂线，与“ $\text{[math]}$ 的l镜像”交于点B、C，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
21. (2021九上·安岳月考) 阅读材料，用配方法求最值.
已知a，b为非负实数，∵ $\text{[math]}$ 0，

∴ $\text{[math]}$ ，当且仅当“a＝b”时，等号成立.示例：当x＞0时，求 $\text{[math]}$ 的最小值；

解： $\text{[math]}$ ，当 $\text{[math]}$ ，即x＝2时，y的最小值为5.
1. （1）若m＞0， $\text{[math]}$ 的最小值为；
2. （2）探究：当x＞0时，求 $\text{[math]}$ 的最小值；
3. （3）如图，已知P为双曲线 $\text{[math]}$ （x＜0）上任意一点，过点P作PB⊥x轴，PA⊥y轴且C（0，﹣4），D（6，0），求四边形ABCD的面积的最小值，并求此时A，B的坐标.
答案解析收藏纠错 + 选题

五、实践探究题

22. (2023·太原模拟) 阅读与思考

下面是小宇同学的一篇日记，请仔细阅读并完成相应的任务．

在物理活动课上，我们“博学”小组的同学，参加了一次“探究电功率P与电阻R之间的函数关系”的活动．

第一步，实验测量．根据物理知识，改变电阻R的大小，通过测量电路中的电流，计算电功率P．

第二步，整理数据．

$\text{[math]}$	…	3	6	9	12	15	…
$\text{[math]}$	…	3	1.5	1	0.75	0.7	…

第三步，描点连线．以R的数值为横坐标，对应P的数值为纵坐标在平面直角坐标系中描出以表中数值为坐标的各点，并用光滑的曲线顺次连接这些点．

在数据分析时，我发现一个数据有错误，重新测量计算后，证明了我的猜想正确，并修改了表中这个数据．实验结束后，大家都有很多收获，每人都撰写了日记．

任务：

（1）表格中错误的数据是，P与R的函数表达式为；
（2）在平面直角坐标系中，画出P与R的函数图象；
（3）结合图象，直接写出P大于6W时R的取值范围．

答案解析收藏纠错 + 选题

23. 在探究欧姆定律时，小明发现小灯泡电路上的电压保持不变，通过小灯泡的电流越大，灯就越亮。设选用小灯泡的电阻为 R(Ω)，通过的电流强度为I(A)(欧姆定律公式： $\text{[math]}$ ）
1. （1）若电阻为40 Ω，通过的电流强度为0.30 A，求Ⅰ关于R的函数表达式.
2. （2）如果电阻小于 40 Ω，那么与(1)中相比，小灯泡的亮度将发生怎样的变化?请说明理由.
答案解析收藏纠错 + 选题

24. (2023九上·七星期中) 如图1，李老师设计了一个探究杠杆平衡条件的实验：在一个自制类似天平的仪器的左边固定托盘 $\text{[math]}$ 中放置一个重物，在右边活动托盘 $\text{[math]}$ （可左右移动）中放置一定质量的砝码，使得仪器左右平衡．改变活动托盘 $\text{[math]}$ 与点 $\text{[math]}$ 的距离 $\text{[math]}$ ，观察活动托盘 $\text{[math]}$ 中砝码的质量 $\text{[math]}$ 的变化情况．实验数据记录如表

$\text{[math]}$	10	15	20	25	30
$\text{[math]}$	30	20	15	12	10

（1）把表中 $\text{[math]}$ 的各组对应值作为点的坐标，在图2的坐标系中描出相应的点，用平滑曲线连接这些点；
（2）观察所画的图象，猜测 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系，求出函数关系式；
（3）当砝码的质量为 $\text{[math]}$ 时，活动托盘 $\text{[math]}$ 与点 $\text{[math]}$ 的距离是多少？

答案解析收藏纠错 + 选题

25. (2023九上·寿阳月考) 阅读与思考
下面是小宇同学的一篇日记，请仔细阅读并完成相应的任务．

在物理活动课上，我们“博学”小组的同学，参加了一次“探究电功率P与电阻R之间的函数关系”的活动．
第一步，实验测量．根据物理知识，改变电阻R的大小，通过测量电路中的电流，计算电功率P．
第二步，整理数据．

R/Ω	…	3	6	9	12	15	…
P/W	…	3	1.5	1	0.75	0.7	…

第三步，描点连线．以R的数值为横坐标，对应P的数值为纵坐标在平面直角坐标系中描出以表中数值为坐标的各点，并用光滑的曲线顺次连接这些点．
在数据分析时，我发现一个数据有错误，重新测量计算后，证明了我的猜想正确，并修改了表中这个数据．实验结束后，大家都有很多收获，每人都撰写了日记．

任务：

（1）表格中错误的数据是，P与R的函数表达式为；
（2）在平面直角坐标系中，画出P与R的函数图象；
（3）结合图象，直接写出P大于6W时R的取值范围．

答案解析收藏纠错 + 选题

26. (2022八下·邗江期末) 模具长计划生产面积为9，周长为m的矩形模具，对于m的取值范围，小陈已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：
1. （1）建立函数模型
  设矩形相邻两边的长分别为 $\text{[math]}$ .由矩形的面积为9，得 $\text{[math]}$ .即 $\text{[math]}$ ；由周长为m，得 $\text{[math]}$ ，即 $\text{[math]}$ ，满足要求的 $\text{[math]}$ .应是两个函数图象在第象限内交点的坐标.
2. （2）画出函数图象
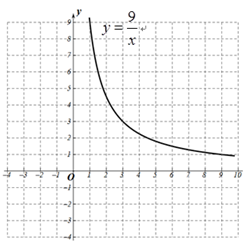
  函数 $\text{[math]}$ 的图象如图所示，而函数 $\text{[math]}$ 的图象可由直线 $\text{[math]}$ 平移得到.请在同一直角坐标系中直接画出直线 $\text{[math]}$ .
3. （3）平移直线 $\text{[math]}$ ，观察函数图象
  ①当直线平移到与函数 $\text{[math]}$ 的图象有唯一交点（3，3），周长m的值为；
  
  ②在直线平移过程中，交点个数还有哪些情况？请写出交点个数及对应的周长m的取值范围；
4. （4）得出结论
  若能生产出面积为9的矩形模具，则周长m的取值范围为
答案解析收藏纠错 + 选题
27. (2023九上·光明月考)
【综合实践】
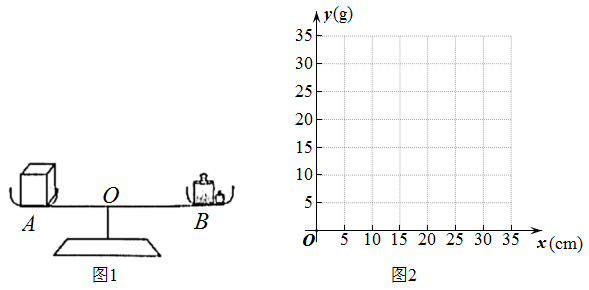
如图所示，是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境（杠杆原理：阻力×阻力臂＝动力×动力臂，如图，即F_A×L₁＝F_B×L₂），受桔槔的启发，小杰组装了如图所示的装置．其中，杠杆可绕支点O在竖直平面内转动，支点O距左端L₁＝1m ，距右端L₂＝0.4m ，在杠杆左端悬挂重力为80N的物体A ．
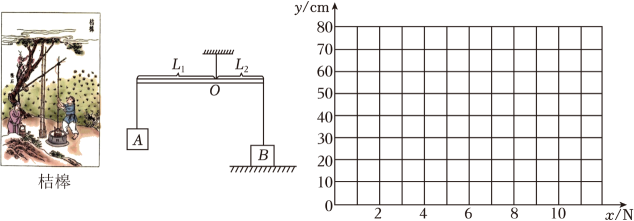
1. （1）若在杠杆右端挂重物B ，杠杆在水平位置平衡时，重物B所受拉力为N ．
2. （2）为了让装置有更多的使用空间，小杰准备调整装置，当重物B的质量变化时，L₂的长度随之变化．设重物B的质量为xN ， L₂的长度为ycm ．则：
  ①y关于x的函数解析式是 ▲ ．
  ②完成下表：
  x/N
  …
  10
  20
  30
  40
  50
  …
  y/cm
  …
  8
  a
  $\text{[math]}$
  2
  b
  …
  ③在直角坐标系中画出该函数的图象．
3. （3）在（2）的条件下，将函数图象向右平移4个单位长度，与原来的图象组成一个新的函数图象，记为L ．若点A的坐标为（2，0），在L上存在点Q ，使得S_△_OAQ＝9．请直接写出所有满足条件的点Q的坐标．
答案解析收藏纠错 + 选题
28. (2023九上·瑞安开学考) 确定有效消毒的时间段
背景素材
预防传染病，某校定期对教室进行“药熏消毒”．已知药物释放阶段，室内每立方米空气中的含药量y（mg）与释放时间x（min）成一次函数；释放后，y与x成反比例如图1所示，且2min时，室内每立方米空气中的含药量y（mg）达到最大值．某兴趣小组记录部分y（mg）与x（min）的测量数据如表1．满足 $\text{[math]}$ 的自变量x（min）的取值范围为有效消毒时间段．
x
…
0.5
1
1.5
2
2.5
3
…
y
…
2.5
3
3.5
4
3.2
2.67
…
问题解决
1. （1）任务1
  确定y关于x的一次函数及反比例函数的表达式．
2. （2）任务2
  初步确定有效消毒时间段即自变量x的取值范围．
3. （3）任务3
  若实际生活中有效消毒时间段要求满足a≤x≤3a ，其中a为常数，请确定实际生活中有效消毒的时间段．
答案解析收藏纠错 + 选题
29. (2024九下·深圳开学考) 【问题背景】
1. （1）数学活动课上，老师拿出一个由五个边长均为1的小正方形连成的L形教具，如图1，将它放入一个直角三角形中，已知∠BCA＝90°，∠B＝30°，顶点D、E、F、G刚好落在三边上，求AB的长；
2. （2）【问题提出与解决】
  小颖同学受到启发，将该教具放入如图2所示的直角坐标系中，顶点A、B、C分别落在坐标轴上，提出问题：如果反比例函数 $\text{[math]}$ （x＜0）图象经过顶点D，求k的值；
3. （3）小明同学也受到启发，画了一个圆，如图3，将该教具放入圆内，使圆经过其顶点A、B、C，提出问题：求该圆的面积．
答案解析收藏纠错 + 选题
30. 数学活动课上，张老师引导同学进行如下探究：将长为 $\text{[math]}$ 的铅笔AB斜靠在垂直于水平桌面AE的直尺FO的边沿上，一端 $\text{[math]}$ 固定在桌面上，图乙是示意图.如图丙所示，将铅笔AB绕端点 $\text{[math]}$ 按顺时针方向旋转，AB与OF交于点 $\text{[math]}$ ，当旋转至水平位置时，铅笔AB的中点 $\text{[math]}$ 与点 $\text{[math]}$ 重合.
1. （1）设 $\text{[math]}$ ，点 $\text{[math]}$ 到OF的距离 $\text{[math]}$ .请回答下列问题：
  ①用含 $\text{[math]}$ 的代数式表示：AD的长是 $\text{[math]}$ 的长是 $\text{[math]}$ ；
  ②写出 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式：，自变量 $\text{[math]}$ 的取值范围是.
2. （2） ①列表：根据第(1)题中求出的函数表达式计算并补全表格；
            $\text{[math]}$
  6
  5
  4
  3.5
  3
  2.5
  2
  1
  0.5
  0
            $\text{[math]}$
  0
  0.55
  1.2
  1.58
  
  2.47
  3
  4.29
  5.08
  
  ②描点：根据表中的数值，在平面直角坐标系(如图丙所示)中描出①中剩余的两个点 $\text{[math]}$ ；
  ③连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象.
3. （3）请你结合函数的图象，写出关于该函数的两条性质或结论.
答案解析收藏纠错 + 选题
31. (2023·深圳模拟) 【项目式学习】
项目主题：守护生命，“数”说安全．
项目背景：随着社会的发展，安全问题变得日益重要．某校为了提高学生的安全意识，开展以“守护生命，'数'说安全”为主题的项目式学习活动．创新小组通过考察测量、模拟探究和成果迁移等环节，开展地下弯道对通行车辆长度的限制研究．
1. （1）任务一：考察测量
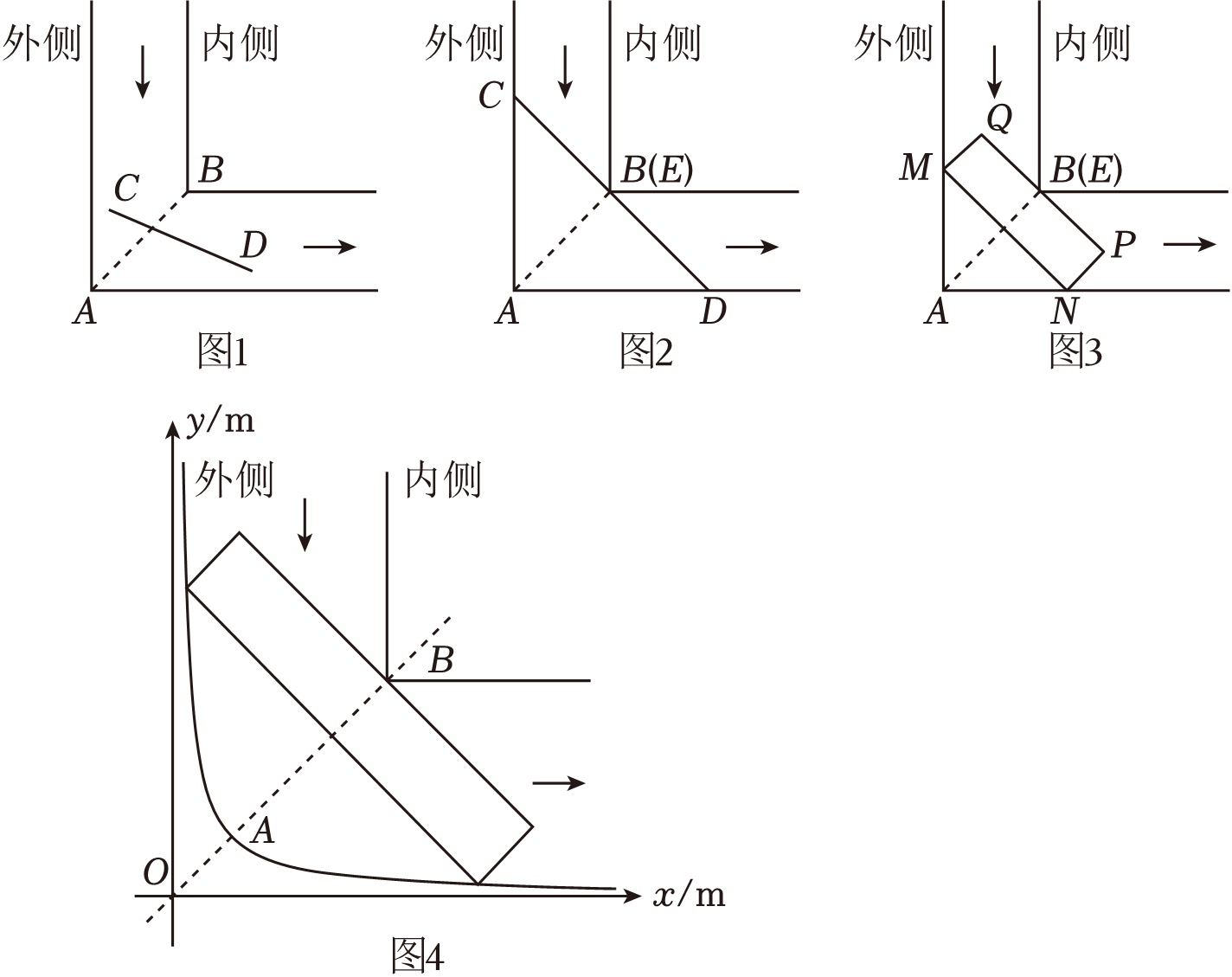
  如图1，创新小组所选取弯道的内、外侧均为直角，道路宽均为4m，则AB＝m；
2. （2）任务二：模拟探究
  如果汽车在行驶中与弯道内、外侧均无接触，则可安全通过．
  创新小组用线段模拟汽车通过宽度相同的直角弯道，探究发现：
  ①当CD＜2AB时（如图1），线段CD能通过直角弯道；
  ②当CD＝2AB时，必然存在线段CD的中点E与点B重合的情况，线段CD恰好不能通过直角弯道（如图2）．此时，∠ADC的度数是；③当CD＞2AB时，线段CD不能通过直角弯道．
3. （3）如图3，创新小组用矩形PQMN模拟汽车通过宽均为4m的直角弯道，发现当PQ的中点E与点B重合，且PQ⊥AB时，矩形PQMN恰好不能通过该弯道．若PQ＝am，PN＝2m，且矩形PQMN能通过该直角弯道，求a的最大整数值．
4. （4）任务三：成果迁移
  如图4，某弯道外侧形状可近似看成反比例函数y＝ $\text{[math]}$ （x＞0）的图象，其对称轴交图象于点A．弯道内侧的顶点B在射线OA上，两边分别与x轴，y轴平行，OA＝2m，AB＝4 $\text{[math]}$ m．创新小组探究发现通过该弯道的原理与通过直角弯道类似．有一辆长为bm，宽为2m的汽车需要安全通过该弯道，则b的最大整数值为．（参考数据： $\text{[math]}$ ≈1.4， $\text{[math]}$ ≈1.7， $\text{[math]}$ ≈2.2， $\text{[math]}$ ≈2.6）
答案解析收藏纠错 + 选题