2024年中考数学精选压轴题之四边形综合探究(一)

更新时间：2024-05-10 浏览次数：53 类型：三轮冲刺

一、解答题

1. (2024八下·潮安期中) 如图，已知正方形ABCD ， AB＝8，点M为射线DC上的动点，射线AM交BD于E ，交射线BC于F ，过点C作CQ⊥CE ，交AF于点Q ．
1. （1）当BE＝2DE时，求DM的长．
2. （2）当M在线段CD上时，若CQ＝3，求MF的长．
3. （3） ①当DM＝2CM时，作点D关于AM的对称点N ，求tan∠NAB的值．
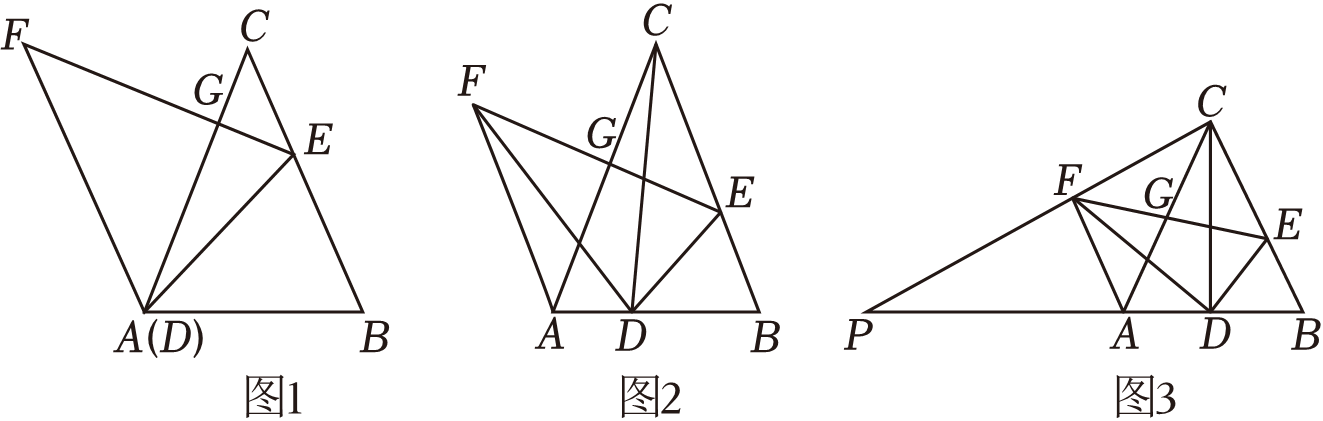
  ②若BE＝4DE ，直接写出△CQE与△CMF的面积比．
答案解析收藏纠错 + 选题
2. (2024八下·岳麓月考) 对于一个四边形给出如下定义：有一组对角相等且有一组邻边相等，则称这个四边形为奇特四边形．
1. （1）命题“另一组邻边也相等的奇特四边形为正方形”是（真或假）命题．
2. （2）如图，在正方形ABCD中，E是AB边上一点，F是AD延长线一点， $\text{[math]}$ ，连接EF ， EC ， FC ，取EF的中点G ，连接CG并延长交AD于点H ．探究：四边形BCGE是否是奇特四边形，如果是证明你的结论，如果不是请说明理由．
3. （3）在（2）的条件下，若四边形BCGE的面积为16，则 $\text{[math]}$ 的值是多少？
答案解析收藏纠错 + 选题
3. (2024八下·临平月考) 如图， $\text{[math]}$ 的对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点O ， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点E ，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ；
  ①若 $\text{[math]}$ ，求平行四边形 $\text{[math]}$ 的面积；
  ②设 $\text{[math]}$ ，试求k与m满足的关系.
答案解析收藏纠错 + 选题
4. (2024八下·诸暨月考) 在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）如图 $\text{[math]}$ ，当 $\text{[math]}$ 时，求对角线 $\text{[math]}$ 的长（用含 $\text{[math]}$ 的式子表示）；
3. （3）如图 $\text{[math]}$ ，四边形 $\text{[math]}$ ，四边形 $\text{[math]}$ 都是平行四边形，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
5. (2024·保康模拟) 在△ABC中，AC＝BC ，点D是边AB上不与点B重合的一动点，将△BDC绕点D旋转得到△EDF ，点B的对应点E落在直线BC上，EF与AC相交于点G ，连接AF ．
1. （1）如图1，当点D与点A重合时，
  ①求证：∠C＝∠CEF；
  ②判断AF与BC的位置关系是 ▲ ；
2. （2）如图2，当点D不与点A重合，点E在边BC上时，判断AF与BC的位置关系，并写出证明过程；
3. （3）如图3，当点D是AB的中点，点E在边BC上时，延长BA ， CF相交于点P ，若AB＝CD＝2，求PF的长．
答案解析收藏纠错 + 选题
6. (2024九下·长春开学考) 如图 $\text{[math]}$ ，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿折线 $\text{[math]}$ 以每秒 $\text{[math]}$ 个单位长度的速度运动，作 $\text{[math]}$ ， $\text{[math]}$ 交边 $\text{[math]}$ 或边 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，当点 $\text{[math]}$ 与点 $\text{[math]}$ 重合时，点 $\text{[math]}$ 停止运动 $\text{[math]}$ 设点 $\text{[math]}$ 的运动时间为 $\text{[math]}$ 秒 $\text{[math]}$
1. （1）当点 $\text{[math]}$ 和点 $\text{[math]}$ 重合时，线段 $\text{[math]}$ 的长为；
2. （2）当点 $\text{[math]}$ 和点 $\text{[math]}$ 重合时，求 $\text{[math]}$ 的比值是多少？
3. （3）当点 $\text{[math]}$ 在边 $\text{[math]}$ 上运动时， $\text{[math]}$ 的形状始终是等腰直角三角形，如图 $\text{[math]}$ ，请说明理由；
4. （4）作点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，当四边形 $\text{[math]}$ 和矩形 $\text{[math]}$ 重叠部分图形为轴对称四边形时，请直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
7. (2024九上·松原期末) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ 点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 方向匀速运动速度为 $\text{[math]}$ ；同时，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 方向匀速运动，速度为 $\text{[math]}$ ；当一个点停止运动时，另一个点也停止运动 $\text{[math]}$ 连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，设运动时间为 $\text{[math]}$ ，解答下列问题：
1. （1）当 $\text{[math]}$ 为何值时， $\text{[math]}$ 是等腰三角形；
2. （2）设五边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，试确定 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式；
3. （3）在运动过程中，当 $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ 时 $\text{[math]}$ 直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
8. (2024九下·黄冈开学考) 已知：在矩形 $\text{[math]}$ 中，把矩形 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，得到矩形 $\text{[math]}$ ，且点 $\text{[math]}$ 落在 $\text{[math]}$ 边上，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）如图 $\text{[math]}$ ，连接 $\text{[math]}$ ．
  $\text{[math]}$ 求证： $\text{[math]}$ 平分 $\text{[math]}$ ；
  $\text{[math]}$ 求证： $\text{[math]}$ 是 $\text{[math]}$ 的中点；
2. （2）如图 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
9. (2023八下·兴仁月考) 在 $\text{[math]}$ 中，B在C的左边， $\text{[math]}$ ，将 $\text{[math]}$ 关于 $\text{[math]}$ 作轴对称，得四边形 $\text{[math]}$ ． P是对角线 $\text{[math]}$ 上的动点， E是直线 $\text{[math]}$ 上的动点，且 $\text{[math]}$ ．
1. （1）四边形 $\text{[math]}$ 如图1所示，四边形 $\text{[math]}$ 是（填“矩形”或“菱形”或“正方形”）； $\text{[math]}$ $\text{[math]}$ （填“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）；
2. （2）四边形 $\text{[math]}$ 如图2所示，且 $\text{[math]}$ ，四边形 $\text{[math]}$ 是 ▲ （填“矩形”或“菱形”或“正方形”）；（1）中 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系还成立吗?若成立，请说明理由．
3. （3）四边形 $\text{[math]}$ 如图3所示，若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的度数．（用含 $\text{[math]}$ 、 $\text{[math]}$ 的代数式表示）
答案解析收藏纠错 + 选题
10. (2024八上·成都期末) 如图1，在边长为2的正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为边在直线 $\text{[math]}$ 右侧作正方形 $\text{[math]}$ ．
图1 图2
1. （1）当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，连接 $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）当点 $\text{[math]}$ 是线段 $\text{[math]}$ 中点，连接 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长；
3. （3）如图2，点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上，连接 $\text{[math]}$ ，若 $\text{[math]}$ 的延长线恰好经过 $\text{[math]}$ 的中点 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
11. (2024九上·武侯期末) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E是 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠得到 $\text{[math]}$ ，边 $\text{[math]}$ ， $\text{[math]}$ 分别交 $\text{[math]}$ 于点M ， N ．
1. （1）求证： $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时．
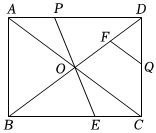
  ①求BE的长；
  ②若点P是 $\text{[math]}$ 边上的动点，连接 $\text{[math]}$ ，过点A作 $\text{[math]}$ 的垂线交线段 $\text{[math]}$ 于点Q ，试探究 $\text{[math]}$ 的值是否发生变化，若变化，请说明理由；若不变，请求出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
12. (2024九上·福州期末) 如图， $\text{[math]}$ 和 $\text{[math]}$ 分别位于 $\text{[math]}$ 两侧， $\text{[math]}$ 为 $\text{[math]}$ 中点，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）如图1，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）如图2，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点F，在 $\text{[math]}$ 上取一点G使得 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ．猜想 $\text{[math]}$ 与 $\text{[math]}$ 之间存在的数量关系，并证明你的猜想；
3. （3）如图3， $\text{[math]}$ 是以 $\text{[math]}$ 为斜边的等腰直角三角形，若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出当 $\text{[math]}$ 取最大值时 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题

二、实践探究题

13. (2024·高州模拟)
1. （1）【问题情境】如图1，四边形ABCD是正方形，点E是AD边上的一个动点，以CE为边在CE的右侧作正方形CEFG，连接DG、BE，则DG与BE的数量关系是；
2. （2）【类比探究】
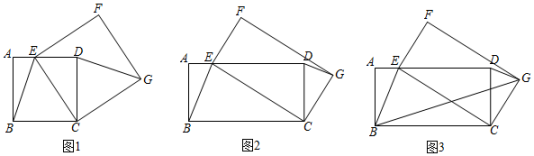
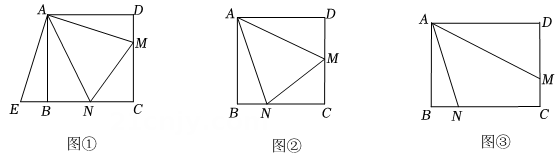
  如图2，四边形ABCD是矩形，AB=2，BC=4，点E是AD边上的一个动点，以CE为边在CE的右侧作矩形CEFG，且CG：CE=1：2，连接DG、BE．判断线段DG与BE有怎样的数量关系和位置关系，并说明理由；
3. （3）【拓展提升】
  如图3，在（2）的条件下，连接BG，则2BG+BE的最小值为．
答案解析收藏纠错 + 选题
14. (2024九下·黄石月考) 综合与实践
1. （1）【思考尝试】
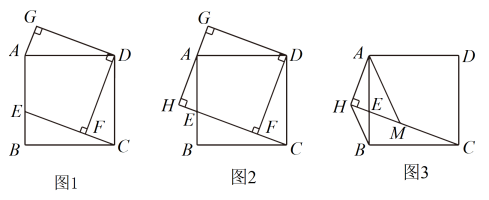
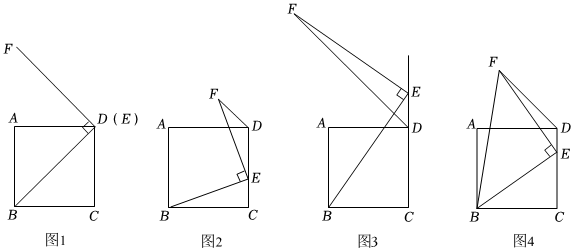
  数学活动课上，老师出示了一个问题：如图1，在矩形ABCD中，E是边 $\text{[math]}$ 上一点， $\text{[math]}$ 于点F， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．试猜想四边形 $\text{[math]}$ 的形状，并说明理由；
2. （2）【实践探究】
  小睿受此问题启发，逆向思考并提出新的问题：如图2，在正方形 $\text{[math]}$ 中，E是边 $\text{[math]}$ 上一点， $\text{[math]}$ 于点F， $\text{[math]}$ 于点H， $\text{[math]}$ 交 $\text{[math]}$ 于点G，可以用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的数量关系，请你思考并解答这个问题；
3. （3）【拓展迁移】
  小博深入研究小睿提出的这个问题，发现并提出新的探究点：如图3，在正方形 $\text{[math]}$ 中，E是边 $\text{[math]}$ 上一点， $\text{[math]}$ 于点H，点M在 $\text{[math]}$ 上，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，可以用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ 的数量关系，请你思考并解答这个问题．
答案解析收藏纠错 + 选题
15. (2024九下·麻城期中) 某校数学活动小组探究了如下数学问题：
1. （1）问题发现：如图1， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．点P是底边 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为腰作等腰 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ 、则 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系是；
2. （2）变式探究：如图2， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．点P是腰 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为底边作等腰 $\text{[math]}$ ，连接 $\text{[math]}$ ，判断 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并说明理由；
3. （3）问题解决：如图3，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是边 $\text{[math]}$ 上一点，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ，点 $\text{[math]}$
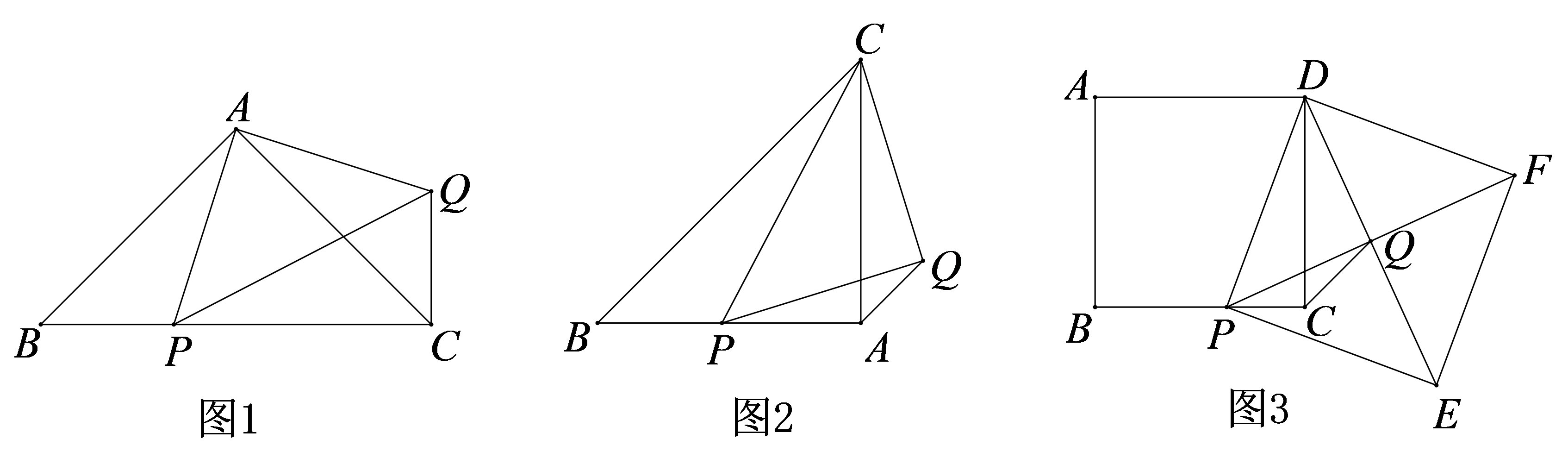
  是正方形 $\text{[math]}$ 两条对角线的交点，连接 $\text{[math]}$ ．若正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出正方形 $\text{[math]}$ 的边长．
答案解析收藏纠错 + 选题
16. (2024·深圳模拟) 综合与探究．
1. （1）【特例感知】
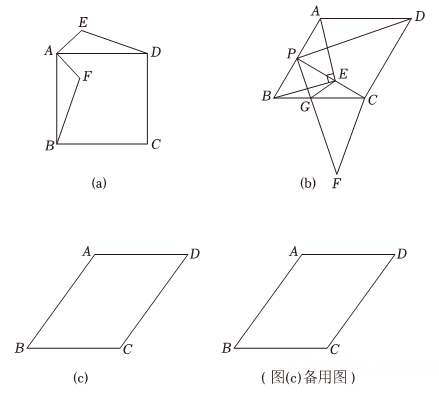
  如图（a），E是正方形ABCD外一点，将线段AE绕点A顺时针旋转 $\text{[math]}$ 得到AF ，连接DE ， BF ．求证： $\text{[math]}$ ；
2. （2）【类比迁移】
  如图（b），在菱形ABCD中， $\text{[math]}$ ， P是AB的中点，将线段PA ， PD分别绕点P顺时针旋转 $\text{[math]}$ 得到PE ， PF ， PF交BC于点G ，连接CE ， CF ，求四边形CEGF的面积：
3. （3）【拓展提升】
  如图（c），在平行四边形ABCD中， $\text{[math]}$ 为锐角且满足 $\text{[math]}$ ． P是射线BA上一动点，点C ， D同时绕点P顺时针旋转 $\text{[math]}$ 得到点 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 为直角三角形时，直接写出BP的长．
答案解析收藏纠错 + 选题
17. (2024九下·随州模拟) 【操作与发现】
如图①，在正方形ABCD中，点N，M分别在边BC、CD上．连接AM、AN、MN．∠MAN=45°，将△AMD绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而可得：DM+BN=MN．
1. （1）【实践探究】在图①条件下，若CN＝6，CM＝8，正方形ABCD的边长是．
2. （2）如图②，在正方形ABCD中，点M、N分别在边DC、BC上，连接AM、AN、MN，∠MAN=45°，若tan∠BAN= $\text{[math]}$ ，，求证：M是CD的中点．
3. （3）【拓展】如图③，在矩形ABCD中，AB=12，AD=16，点M、N分别在边DC、BC上，连接AM、AN，已知∠MAN=45°，BN=4，则DM的长是．
答案解析收藏纠错 + 选题
18. (2024九下·广州月考) 问题提出：如图（1）， $\text{[math]}$ 是菱形 $\text{[math]}$ 边 $\text{[math]}$ 上一点， $\text{[math]}$ 是等腰三角形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，探究 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系．问题探究：
1. （1）先将问题特殊化，如图（2），当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的大小；
2. （2）再探究一般情形，如图（1），求 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系；
3. （3）问题拓展将图（1）特殊化，如图（3），当 $\text{[math]}$ 时，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
19. (2024九下·深圳月考)
1. （1）【问题探究】如图1，正方形ABCD中，点F、G分别在边BC、CD上，且AF⊥BG于点P ，求证：AF＝BG；
2. （2）【知识迁移】如图2，矩形ABCD中，AB＝4，BC＝8，点E、F、G、H分别在边AB、BC、CD、AD上，且EG⊥FH于点P ．若EG•HF＝48，求HF的长；
3. （3）【拓展应用】如图3，在菱形ABCD中，∠ABC＝60°，AB＝6，点E在直线AB上，BE＝4，AF⊥DE交直线BC于点F ．请直接写出线段FC的长．
答案解析收藏纠错 + 选题
20. (2024·广西壮族自治区模拟)
【活动探究】在数学课上，老师出示了一个问题：如图1，在菱形ABCD中， $\text{[math]}$ ，点E，F分别是BC，CD边上一点，若 $\text{[math]}$ ，试猜想 $\text{[math]}$ 的形状，不用证明．
【尝试实践】小美受此启发，她尝试将“ $\text{[math]}$ ”改为“ $\text{[math]}$ ”，通过测量验证发现猜想仍然成立，并进一步思考证法：如图2，过点 $\text{[math]}$ 作 $\text{[math]}$ ，求证 $\text{[math]}$
请你按照小美的思路进一步思考，并解答这个问题．
【拓展应用】小玲在老师问题上进一步改编：如图3，过 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，当EF的中点 $\text{[math]}$ 经过CG时，请直接写出EF的长度．

答案解析收藏纠错 + 选题
21. (2024八上·海曙期末) 定义：把斜边重合，且直角顶点不重合两个直角三角形叫做共边直角三角形．
1. （1）概念理解：如图1，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ，说明 $\text{[math]}$ 和 $\text{[math]}$ 是共边直角三角形．
2. （2）问题探究：如图2， $\text{[math]}$ 和 $\text{[math]}$ 是共边直角三角形，E、F分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ，求证 $\text{[math]}$ ．
3. （3）拓展延伸：如图3， $\text{[math]}$ 和 $\text{[math]}$ 是共边直角三角形，且 $\text{[math]}$ ，连结 $\text{[math]}$ ，求证： $\text{[math]}$ 平分 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2024九上·松原期末) 综合与探究
问题情境：数学课上，老师引导同学们以“正方形中线段的旋转”为主题开展数学活动 $\text{[math]}$ 已知正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上一点 $\text{[math]}$ 不与点 $\text{[math]}$ 重合 $\text{[math]}$ ，连接 $\text{[math]}$ 将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）特例分析：如图 $\text{[math]}$ ，当点 $\text{[math]}$ 与点 $\text{[math]}$ 重合时，求 $\text{[math]}$ 的度数；
2. （2）深入探究：当点 $\text{[math]}$ 不与点 $\text{[math]}$ 重合时， $\text{[math]}$ 中的结论是否仍然成立？若成立，请在图 $\text{[math]}$ 与图 $\text{[math]}$ 中选择一种情况进行证明：若不成立，请说明理由；
3. （3）问题解决：如图 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，且 $\text{[math]}$ 时，请直接写出线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
23. (2024九上·威宁期末) 定义：长宽比为 $\text{[math]}$ （n为正整数）的矩形称为 $\text{[math]}$ 矩形．下面，我们通过折叠的方式折出一个 $\text{[math]}$ 矩形，如图①所示．
操作1：将正方形 $\text{[math]}$ 沿过点 $\text{[math]}$ 的直线折叠，使折叠后的点 $\text{[math]}$ 落在对角线 $\text{[math]}$ 上的点 $\text{[math]}$ 处，折痕为 $\text{[math]}$ ．
操作2：将 $\text{[math]}$ 沿过点 $\text{[math]}$ 的直线折叠，使点 $\text{[math]}$ ，点 $\text{[math]}$ 分别落在边 $\text{[math]}$ ， $\text{[math]}$ 上，折痕为 $\text{[math]}$ ．
则四边形 $\text{[math]}$ 为 $\text{[math]}$ 矩形．
证明：设正方形 $\text{[math]}$ 的边长为1，则 $\text{[math]}$ ．
由折叠性质可知 $\text{[math]}$ ， $\text{[math]}$ ，则四边形 $\text{[math]}$ 为矩形，
∴ $\text{[math]}$ ， ∴ $\text{[math]}$ ．
∴ $\text{[math]}$ ，即 $\text{[math]}$ ， ∴ $\text{[math]}$ ， ∴ $\text{[math]}$ ，
∴四边形 $\text{[math]}$ 为 $\text{[math]}$ 矩形．
阅读以上内容，回答下列问题：
1. （1）在图①中，所有与 $\text{[math]}$ 相等的线段是、， $\text{[math]}$ 的值是；
2. （2）已知四边形 $\text{[math]}$ 为 $\text{[math]}$ 矩形，模仿上述操作，得到四边形 $\text{[math]}$ ，如图②，求证：四边形 $\text{[math]}$ 为 $\text{[math]}$ 矩形；
3. （3）将图②中的 $\text{[math]}$ 矩形 $\text{[math]}$ 沿用（2）中的方式操作3次后，得到一个“ $\text{[math]}$ 矩形”，则 $\text{[math]}$ 的值是．
答案解析收藏纠错 + 选题
24. (2024八上·播州期末) 【提出问题】如图 $\text{[math]}$ ，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ，分别以 $\text{[math]}$ ， $\text{[math]}$ 为边作等边 $\text{[math]}$ 和等边 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）【初步探究】如图 $\text{[math]}$ ，连接 $\text{[math]}$ ，求证： $\text{[math]}$ ≌ $\text{[math]}$ ．
2. （2）【深入探究】如图 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，类比 $\text{[math]}$ 的探究方法发现：
  结论 $\text{[math]}$ ：_▲_≌ $\text{[math]}$ ；
  结论 $\text{[math]}$ ： $\text{[math]}$ ．
  请证明结论 $\text{[math]}$ ．
3. （3）如图 $\text{[math]}$ 、在 $\text{[math]}$ 的情况下将线段 $\text{[math]}$ 沿 $\text{[math]}$ 翻折得到线段 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，试判断线段 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系．
答案解析收藏纠错 + 选题