综合与实践数学活动课上,张老师给出了一个问题:
已知二次函数y=x2+2x-3,当-2≤x≤2时,y的取值范围为;
①小伟同学经过分析后,将原二次函数配方成y=a(x-h)2+k
形式,确定抛物线对称轴为直线x=h , 通过-2、h和2的大小
关系,分别确定了最大值和最小值,进而求出y的取值范围;
②小军同学画出如图的函数图象,通过观察图象确定了y的取值范围;请你根据上述两名同学的分析写出y的取值范围是;
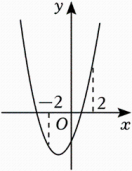
张老师发现两名同学分别从“数”和“形”的角度分析、解决问题,为了让同学们更好感悟“数形结合”思想,张老师将前面问题变式为下面问题,请你解答:已知二次函数y=-x2+2x-3,当-2≤x≤2时,求y的取值范围;
已知二次函数y=-x2+6x-5,当a≤x≤a+3时,二次函数的最大值为y1 , 最小值为y2 , 若y1-y2=3,求a的值.
绿化带灌溉车的操作方案
素材1 | 辆绿化带灌溉车正在作业,水从喷水口喷出,水流的上下两边缘可以抽象为两条抛物线的一部分:喷水口离开地面高1.6米,上边缘抛物线最高点离喷水口的水平距离为3米,高出|喷水口0.9米,下边缘水流形状与上边缘相同,且喷水口是最高点。 |
|
素材2 | 路边的绿化带宽4米 | |
素材3 | 绿化带正中间种植了行道树,为了防治病虫害、增加行道树的成活率,园林工人给树木“打针”。针一般打在离地面1.5米到2米的高度(包含端点)。 |
|
问题解决
建立如图所示直角坐标系,求上边缘抛物线的函数表达式.
灌溉车行驶过程中喷出的水能浇浓到整个绿化带吗?请说明理由.
灌溉时,发现水流的上下两边缘冲击力最强,喷到针筒容易造成针筒脱落。那么请问在满足最大灌溉面积的前提下对行道树“打针”是否有影响,并说明理由;若你认为有影响,请给出具体的“打针”范围。
素材1 图1是中国传统建筑——凉亭,其截面为两个成轴对称的抛物线的一部分(如图2).凉亭外延水平宽度EC为6米,亭高AO=4米,在抛物线最低处由一根高为3.1米的柱子支撑,柱子离亭正中心O点距离为2.4米;

素材2 为了美观,拟在凉亭右侧抛物线内悬挂一盏上下长度为0.5米,左右宽度为0.2米的灯笼(如图3),要使得整个灯笼处于右侧且保持离地至少3米的安全距离(灯笼挂钩G位于其中间最上端).


素材1 图1为某公园的抛物线型拱桥,图2是其横截面示意图,测得水面宽度米,拱顶离水面的距离为
米.
素材2 拟在公园里投放游船供游客乘坐,载重最少时,游船的横截面如图3所示,漏出水面的船身为矩形,船顶为等腰三角形.测得相关数据如下:米,
米,
米,
米.
素材3 为确保安全,拟在石拱桥下面的P,Q两处设置航行警戒线,要求如下:
①游船底部在P,Q之间通行;
②当载重最少通过时,游船顶部E与拱桥的竖直距离至少为米.
确定文具套餐售价 | |
素材1 | 某书店销售一款文具套装,当每套文具售价为30元时,月销售量为200套,经市场调查表明,每套文具售价每降价1元,则月销售量增加20套.设每套文具的售价为x元(x为正整数),月销售量为y套. |
素材2 | 该文具套装的成本是10元/套. |
素材3 | 为促进公益,在售价不低于进价且每套文具获利不高于95%的前提下,该书店决定,每月捐赠400元给慈善机构. |
问题解决:
求y关于x的函数表达式.
当售价为多少时,月利润W获得最大?最大利润是多少?
为了保证捐款后月利润不低于3040元,文具套装的售价可以取哪些数值.
如何设计喷泉喷头的升降方案? | ||||||||||||
素材1 | 如图,有一个可垂直升降的喷泉,喷出的水柱呈抛物线.记水柱上某一点到喷头的水平距离为x米,到湖面的垂直高度为y米.当喷头位于起始位置时,测量得x与y的四组数据如下:
|
| ||||||||||
素材2 | 公园想设立新的游玩项目,通过升降喷头,使游船能从水柱下方通过,如图,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.4米.已知游船顶棚宽度为2.8米,顶棚到湖面的高度为2米. |
| ||||||||||
问题解决 | ||||||||||||
任务1 | 确定喷泉形状 | 结合素材1,求y关于x的表达式. | ||||||||||
任务2 | 探究喷头升降方案 | 为使游船按素材2要求顺利通过,求喷头距离湖面高度的最小值. | ||||||||||
如何设计喷水装置的高度? | ||
素材1 | 如图1为某公园的圆形喷水池,图2是其示意图,O为水池中心,喷头A、B之间的距离为20米,喷射水柱呈抛物线形,水柱距水池中心 | |
|
| |
素材2 | 如图3,拟在圆柱形蓄水池中心处建一喷水装置 ①不能碰到图2中的水柱; ②落水点G,M的间距为 ③水柱的最高点与点P的高度差为 ④从点P向四周喷射与图2中形状相同的抛物线形水柱. |
|
问题解决 | ||
任务1 | 确定水柱形状 | 在图2中以点O为坐标原点,水平方向为x轴建立直角坐标系,并求这条抛物线的函数表达式. |
任务2 | 探究落水点位置 | 在建立的坐标系中,求落水点G的坐标. |
任务3 | 拟定喷水装置的高度 | 求出喷水装置 |
素材 | 内容 |
素材1 | 高脚杯:如图1,类似这种杯托上立着一只细长脚的杯子.从下往上分为三部分:杯托,杯脚,杯体.杯托为一个圆;水平放置时候,杯脚经过杯托圆心,并垂直任意直径;杯体的水平横截面都为圆,这些圆的圆心都在杯脚所在直线上. |
素材2 | 图2坐标系中,特制男士杯可以看作线段AB , OC , 抛物线DCE(实线部分),线段DF , 线段EG绕y轴旋转形成的立体图形(不考虑杯子厚度,下同). 图2坐标系中,特制女士杯可以看作线段AB , OC , 抛物线FCG(虚线部分)绕y轴旋转形成的立体图形. |
素材3 | 已知,图2坐标系中,OC=50mm , 记为C(0,50),D(﹣25,75),E(25,75),F(﹣25,150),G(25,150). |
根据以上素材内容,尝试求解以下问题:
如何设计种植方案? | |||||||||||||||
素材1 | 某校为响应国家政策,在校内100平方米的土地上进行种植课实践,现有A、B,C三种作物的相关信息如表所示.已知5株A作物和2株B作物的产量共为7千克:10株A作物和6株B作物的产量共为15千克.
| ||||||||||||||
素材2 | 由于A作物植株间距较大,可增加A作物每平方米的种植株树.经过实验发现,每平方米种植A作物每增加1株,A作物的单株产量减少0.1千克.而B,C单株产量不发生变化. | ||||||||||||||
素材3 | 若同时种植A,B,C三种作物,实行分区域种植. | ||||||||||||||
问题解决 | |||||||||||||||
任务1 | 确定单株产量 | 求x,y的值. | |||||||||||||
单一种植(全部种植A作物) | 任务2 | 预估种植策略 | 要使A作物每平方米产量为4千克,则每平方米应种植多少株? | ||||||||||||
分区种植(种植A,B,C三种作物) | 任务3 | 规划种植方案 | 设这100平方米的土地中有a平方米用于种植A作物,且每平方米的产量最大:有b平方米用于种植B作物,剩余的全用来种植C作物,a,b均为正整数.当这100平方米总产量为577千克时,求这三种作物的种植方案. | ||||||||||||
问题提出:某兴趣小组开展综合实践活动:在中,
, D为
上一点,
, 动点P以每秒1个单位的速度从C点出发,在三角形边上沿
匀速运动,到达点A时停止,以
为边作正方形
设点P的运动时间为
, 正方形
的面积为S , 探究S与t的关系.

①当时,
.
②S关于t的函数解析式为.
① ▲ ;
②当时,求正方形
的面积.
《蔬菜大棚的设计》 | ||
驱动问题 | 1、如何利用函数模型,刻画蔬菜大棚的棚面? 2、如何安装排气装置,保证蔬菜大棚的通风性? 3、如何设计大棚间距,保障蔬菜大棚的采光性? | |
项目背景 | 蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它出现使得人们可以吃到反季节蔬菜.如图,一般蔬菜大棚使用竹结构或者钢结构的骨架,这样就形成了一个温室空间.
| |
数学建模 | 如图,某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成,其中AB=3m,取BC中点O,过点O作线段BC的垂直平分线OE交抛物线AED于点E,BC所在直线为x轴,OE为y轴建立如图所示平面直角坐标系.抛物线AED的顶点E(0,4) |
|
问题解决 | 如图,为了保证该蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置LFGT,若FL=NR=0.75m,求两个正方形装置的间距GM的长. |
|
问题解决 | 为了保证两个蔬菜大棚间的采光不受影响,如图,在某一时刻,此时大棚截面的阴影为CK,求CK的长. |
|
素材1 | 如图1,空地上有两条互相垂直的小路OP,OQ,中间有一正方形ABCD水池,已知水池的边长为4 米,AB//OQ,AD//OP,且AB与OQ的距离为10 米,AD与OP的距离为8 米. |
| ||
素材2 | 现利用两条小路,再购置30 米长的栅栏(图中的细实线)在空地上围出一个花圃,要求围起来的栅栏与小路相互平行(或垂直),靠小路和水池的都不需要栅栏,接口损耗忽略不计. | |||
| 任务1 | 任务2 | ||
| 小明同学按如图2的设计,若EF=16米,求出花圃的面积(不包含水池的面积).
| 若按如图3、如图4设计方案,通过计算说明哪种方案的最大面积更大.
| ||
项目反 思 | 如果栅栏不一定与墙面垂直(或平行),你还能设计出比以上方案面积更大的花圃吗?某学习小组在探究的过程中,设计了方案如图5,你认为图5的最大面积与以上方案比较,哪个更大,请通过计算说明. |
| ||
测算石拱桥拱圈的半径 | ||
素材1 | 某数学兴趣小组测算一座石拱桥拱圈的半径(如图1),石拱桥由矩形的花岗岩叠砌而成,上、下的花岗岩错缝连接(花岗岩的各个顶点落在上、下花岗岩各边的中点,如图2所示). | |
素材2 | 通过观察发现A,B,C三个点都在拱圈上,A是拱圈的最高点,且在两块花岗岩的连接处,B,C两个点都是花岗岩的顶点(如图3). | |
素材3 | 如果没有带测量工具,那么可以用身体的“尺子”来测,比如前臂长(包括手掌、手指)(如图4),利用该方法测得一块花岗岩的长和宽(如图5). | |
问题解决 | ||
任务1 | 获取数据 | 通过观察、计算B,C两点之间的水平距离及铅垂距离(高度差). |
任务2 | 分析计算 | 通过观察、计算石拱桥拱圈的半径. |
注:测量、计算时,都以“肘”为单位.
设计货船通过圆形拱桥的方案 | ||
素材1 | 图1中有一座圆拱石桥,图2是其圆形桥拱的示意图,测得水面宽AB=16m,拱顶离水面的距离CD=4m.
| |
素材2 | 如图3,一艘货船露出水面部分的横截面为矩形EFGH,测得EF=3m,EH=10m.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度y(米)与货船增加的载重量x (吨)满足函数关系式y=
| |
问题解决 | ||
任务1 | 确定桥拱半径 | 求圆形桥拱的半径. |
任务2 | 拟定设计方案 | 根据图3状态,货船能否通过圆形桥拱?若能,最多还能卸载多少吨货物?若不能,至少要增加多少吨货物才能通过? |
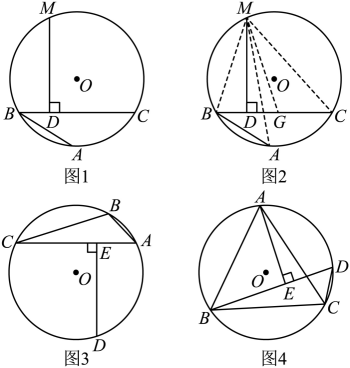
阿拉伯Al-Binmi(973年一1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Binmi译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
小明同学运用“截长法”和三角形全等来证明CD=AB+BD,过程如下:
证明:如图2所示,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,∴MA=MC,…

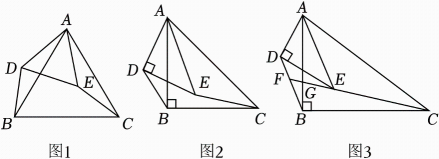
如图1,在中,D , E分别在
,
上,连结DE,若
, 求证:
.
如图2,在中,在
上取一点E , 以
为一边构造平行四边形
, 使点D , F恰好落在
,
上,连结
, 若
,
,
, 求
的长.
如图3,在中,在
上取一点E , 以
为一边构造平行四边形
, 使点F恰好落在
上,连结
,
, 若
,
,
,
, 求
的长。
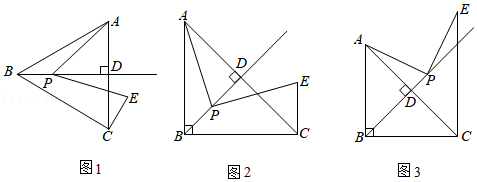
①求的值;
②延长CE交BD于点F,交AB于点G.若 , AB=6,求BF的长.

如图①,在矩形中,
,
分别交
于点E、F,
分别交
于点G、H,求证:
;


如图1,在正方形ABCD中,AC,BD是对角线,点在AB边上,点
在对角线AC上,
, 求证:
.
如图2,在矩形ABCD中, , 点
在AB边上,点
在对角线AC上,
, 求CF的长
如图3,在菱形ABCD中, , 点
在AB边上,点
在对角线AC上,
, 作
交DA的延长线于点H,DE的延长线交BH于点
, 请直接写出BP,BE的长.
