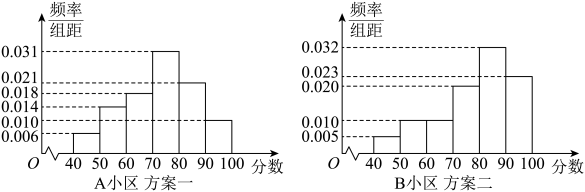
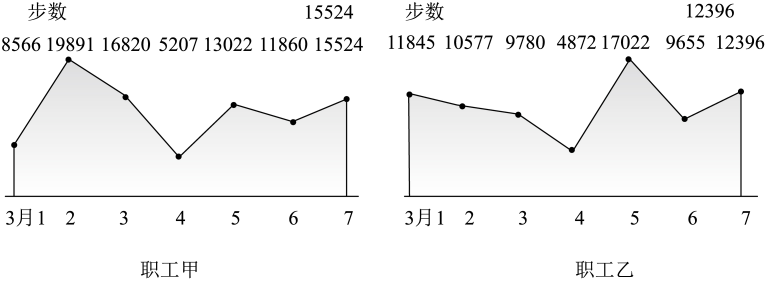
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳形,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为
.假设数据在组内均匀分布.以事件发生的频率作为相应事件发生的概率.
| B学科良好 | B学科不够良好 | 合计 |
A学科良好 | |||
A学科不够良好 | |||
合计 |
附: , 其中
.
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | 0.15 | |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | 2.072 |

非“运动达人” | “运动达人” | 合计 | |
男性 | 15 | 45 | |
女性 | |||
合计 |
附: , n=a+b+c+d,
临界值表:
p(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
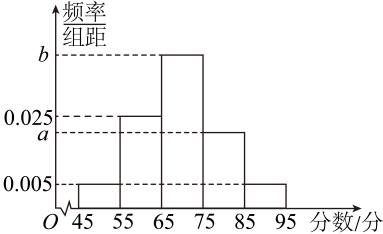

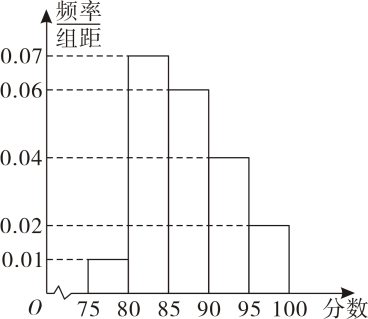

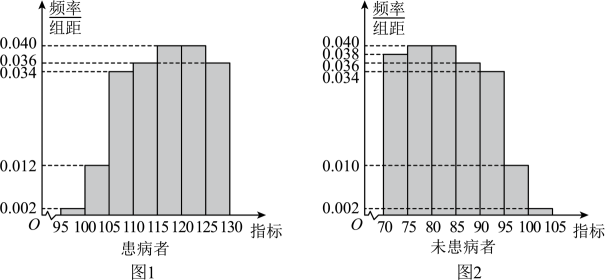
利用该指标制定一个检测标准,需要确定临界值 , 将该指标大于
的人判定为阳性,小于或等于
的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为
;误诊率是将未患病者判定为阳性的概率,记为
. 假设数据在组内均匀分布.


为了研究每天的游客数是否和当天的最高气温有关,从这一百天中随机抽取了天,统计出这
天的游客数
千人
分别为
、
、
、
、
, 已知这
天的最高气温
依次为
、
、
、
、
.
参考公式:由最小二乘法所得回归直线的方程是;其中:
,
.
本题参考数据: ,
.
|
|
感兴趣 |
不感兴趣 |
合计 |
|
男生 |
|||
|
女生 |
|||
|
合计 |
附:参考公式: , 其中
.
临界值表:
|
|
0.15 |
0.10 |
0.05 |
0.01 |
0.005 |
|
|
2.072 |
2.706 |
3.841 |
6.635 |
7.879 |

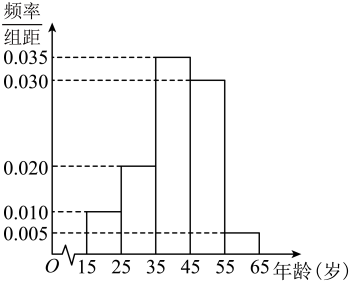
①若有甲年龄
, 乙
年龄
两人已确定人选宣传使者,现计划从第一组和第五组被抽到的使者中,再随机抽取
名作为组长,求甲、乙两人恰有一人被选上的概率;
②若第四组宣传使者的年龄的平均数与方差分别为和
, 第五组宣传使者的年龄的平均数与方差分别为
和
, 据此估计这
人中
岁所有人的年龄的方差.


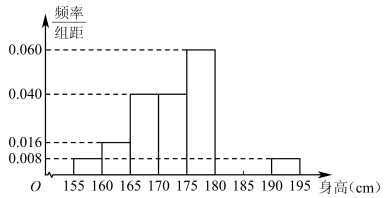

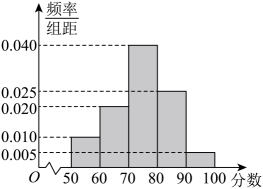
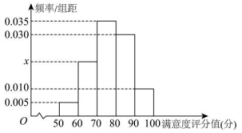
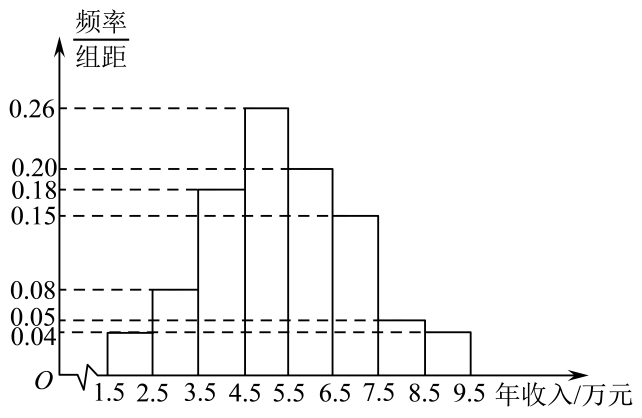
①将y表示为x的函数;
②以频率估计概率,标准差s精确到1,根据频率分布直方图估计且y不少于68万元的概率.


附:若随机变量服从正态分布
, 则
,
,
.


①;
② .

参考数据:若X~N(μ , σ2),则P(μ-σ<X≤μ+σ)≈0.68,P(μ-2σ<X≤μ+2σ)≈0.95,P(μ-3σ<X≤μ+3σ)≈0.99.
附:若随机变量服从正态分布
, 则: