备考2024年中考数学重难创新题5 圆的综合题

如图，AB是⊙O的直径，点C为弧BD的中点，连结AC交BD于点E，CE＝1， ，老师要求同学们在矩形方框中添加一个条件和结论后，编制成一道完整的题目，并解答.

如图，△ABC内接于⊙O，直径AB的长为2，过点C的切线交AB的题长线于点D.张老师要求添加条件后，编制一道题目，并解答。

任务：

已知：和圆外一点P．

求作：过点P的的切线．

作法：①连接；作的垂直平分线与交于点M；②以半径作 ， 交于点A，B；③作直线；

所以直线为的切线．

请利用尺规作图补全小文的作图过程，并完成下面的证明．

证明：连接 ．

∵为的直径，

∴      ▲ =      ▲ （      ）（填推理的依据）．

∴

∵为半径，

∴直线为的切线．（      ）（填推理的依据）．

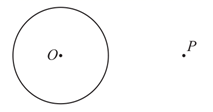
根据小文设计的作图过程，完成下面的证明．

证明：连接 ， ．

∵ 为 的直径，

∴ =∠     ▲      =  ▲   º

（  ▲   ）（填推理的依据）．

∴ ，  ▲   ．

∵ ， 为 的半径，

∴直线 ， 为 的切线（  ▲   ）（填推理的依据）．

发现：

（1）若干平面上三点能够确定一个圆，那么这三点所满足的条件．

（2）我们判断四个点A，B，C，D（任意其中个三点不共线）是否在同一圆上时，一般地，先作过A，B，C三点的圆，然后判断点D是否在这个圆上，如果在，则这四个点共圆，如果不在，则不存在同时过这四个点的圆．

思考：

（1）如图1，∠ACB=∠ADB=90°，那么点A，B，C，D四点在不在同一个圆上；

（2）如图2，如果∠ACB=∠ADB=a（a≠90°），（点C，D在AB的同侧），那么点D还在经过A，B，C三点的圆上吗？芳芳已经证明了点D不在圆内（如图所示），只要能够证明点D也不再圆外，就可以判断点D一定在圆上了，请你完成证明过程．

芳芳的证明过程：

如图3，过A，B，C三点作圆，圆心为O．假设点D在⊙O内，设AD的延长线交⊙O于点P，连接BP．易得∠APB=∠ACB．又由∠ADB是△BPD的外交，得到∠ADB＞∠APB，因此∠ADB＞∠ACB，这个结论与条件中的∠ACB=∠ADB矛盾，所以点D不在圆内．

应用：

如图4，在四边形ABCD中，连接AC，BD，∠CAD=∠CBD=90°，点P在CA的延长线上，连接DP．若∠ADP=∠ABD．求证：DP为Rt△ACD的外接圆的切线．

人类会作圆并且真正了解圆的性质是在2000多年前，由我国的墨子给出圆的概念：“一中同长也．”．意思说，圆有一个圆心，圆心到圆周的长都相等．这个定义比希腊数学家欧几里得给圆下的定义要早100年．与圆有关的定理有很多，弦切角定理就是其中之一．

我们把顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．

弦切角定理：弦切角的度数等于它所夹弧所对的圆周角度数．

下面是弦切角定理的部分证明过程：

证明：如图①，AB与⊙O相切于点A．当圆心O在弦AC上时，容易得到∠CAB＝90°，所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数．

如图②，AB与⊙O相切于点A ， 当圆心O在∠BAC的内部时，过点A作直径AD交⊙O于点D ， 在上任取一点E ， 连接EC ， ED ， EA ， 则∠CED＝∠CAD．

任务：

下面是运用“截长法”证明的部分证明过程.

证明：如图2，在上截取 ， 连接和.

∵M是的中点，

 ∴

任务：

请阅读下列材料，并完成相应的任务．

任务：

九年级学生小刚喜欢看书，他在学习了圆后，在家里突然看到某本数学书上居然还有一个相交弦定理（圆内的两条相交弦，被交点分成的两条线段长的积相等），下面是书上的证明过程，请仔细阅读，并完成相应的任务．

任务：

阿基米德折弦定理

阿基米德（Arehimedes，公元前287—公元前212年，古希腊）是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子．

阿拉伯Al-Biruni（973年—1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》，第一题就是阿基米德的折弦定理．

阿基米德折弦定理：如图1，AB和BC是的两条弦（即折线ABC是圆的一条折弦）， ， M是的中点，则从点M向BC所作垂线的垂足D是折弦ABC的中点，即 ．

这个定理有很多证明方法，下面是运用“垂线法”证明的部分证明过程．

证明：如图2，过点M作射线AB，垂足为点H，连接MA，MB，MC．

∵M是的中点，

∴ ．

…

任务：

阿基米德折弦定理

阿基米德（Archimedes，公元前287~公元212年，古希腊是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子.

阿拉伯Al-Biruni（973年-1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》，第一题就是阿基米德的折弦定理.

阿基米德折弦定理：如图1， 和 是 的两条弦（即折线 是圆的一条折弦）， ， 是 的中点，则从点 向 所作垂线的垂足 是折弦 的中点，即 ，

下面是运用“补短法”证明 的部分证明过程.

证明：如图2，延长 到点F，使得 ，连接DA，DB，DC和DF.

∵ 是 的中点

∴

…

任务：

①用尺规作图法找出 所在圆的圆心(保留作图痕迹，不写作法)；

②设△ABC是等腰三角形，底边BC＝8cm，腰AB＝5cm，求圆片的半径R.

在Rt△ABC中，∠C=90°．

（1）用尺规作图作Rt△ABC的重心P．（保留作图痕迹，不要求写作法和证明）；

（2）你认为只要知道Rt△ABC哪一条边的长即可求出它的重心与外心之间的距离？并请你说明理由．

我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB的最小覆盖圆就是以线段AB为直径的圆．

（1）请分别作出下图中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；

（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）．

已知：点A在上．

求作：的切线 ．

作法： ①作射线；

②以点A为圆心，适当长为半径作弧，交射线于点C和点D；

③分别以点C，D为圆心，大于长为半径作弧，两弧交点B；

④作直线 ．

则直线即为所求作的的切线.

根据小美设计的尺规作图过程，解决下面的问题：

已知：如图1， ．

求作：等边 ， 使得等边内接于 ．

作法：

①如图2，作半径；

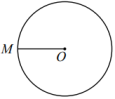
②以M为圆心，长为半径作弧，交于点A，B，连接；

③以B为圆心，长为半径作弧，交于点C；

④连接 ， ．

∴就是所求作的等边三角形．

根据上述尺规作图的过程，回答以下问题：

已知：如图，⊙O．

求作：⊙O的内接正方形．

作法：① 作⊙O的直径AB；

② 分别以点A，B为圆心，大于AB同样长为半径作弧，两弧交于M，N；

③ 作直线MN交⊙O于点C，D；

④ 连接AC，BC，AD，BD．

∴ 四边形ACBD就是所求作的正方形．

根据小明设计的尺规作图过程，

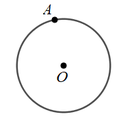
已知：点A在上．

求作：直线PA和相切．

作法：如图，

①连接AO；

②以A为圆心，AO长为半径作弧，与的一个交点为B；

③连接BO；

④以B为圆心，BO长为半径作圆；

⑤作的直径OP；

⑥作直线PA．

所以直线PA就是所求作的的切线．

根据小亮设计的尺规作图过程，

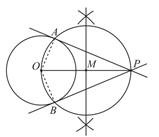
已知：如图，⊙O及⊙O上一点P．

求作：过点P的⊙O的切线．

作法：如图，作射线OP；

① 在直线OP外任取一点A，以A为圆心，AP为半径作⊙A，与射线OP交于另一点B；

②连接并延长BA与⊙A交于点C；

③作直线PC；

则直线PC即为所求．根据小元设计的尺规作图过程，

已知：⊙O

求作：矩形ABCD，使得矩形ABCD内接于⊙O，且其对角线AC，BD的夹角为60°．

作法：如图

①作⊙O的直径AC；

②以点A为圆心，AO长为半径画弧，交直线AC上方的圆弧于点B；

③连接BO并延长交⊙O于点D；

所以四边形ABCD就是所求作的矩形．

根据小东设计的尺规作图过程，

尺规作图：过圆外一点作圆的切线．

已知： 为 外一点．

求作：经过点 的 的切线．

小敏的作法如下：

①连接 ，作线段 的垂直平分线 交 于点 ；

②以点 为圆心， 的长为半径作圆，交 于 两点；

③作直线 ．所以直线 就是所求作的切线．

根据小敏设计的尺规作图过程．

已知：在△ABC中，AB=BC，BD平分∠ABC交AC于点D．

求作：∠BPC，使∠BPC=∠BAC．

作法：① 分别以点B和点C为圆心，大于的长为半径作弧，两弧交于点E和点F，

连接EF交BD于点O；

② 以点O为圆心，OB的长为半径作⊙O；

③ 在劣弧AB上任取一点P（不与点A、B重合），连接BP和CP．所以∠BPC=∠BAC．

根据小玟设计的尺规作图过程．