
①若∠BME=25°,∠END=75°,则∠H的度数为 ▲ ;
②探究∠MEN与∠MHN的数量关系,并给予证明;



①若∠A=20°,∠D=50°,则∠AED= ▲ 度;
②若∠A=35°,∠D=45°,则∠AED= ▲ 度;
③猜想图1中∠AED、∠EAB、∠EDC的数量关系并证明你的结论.
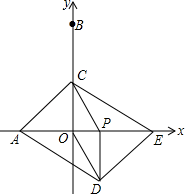
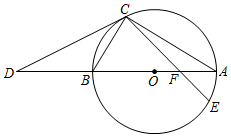
如图2,射线FE与长方形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方),P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(直接写出结论,不要求证明)

①求的度数;
②若 , 求
的度数.




答:_(填“一致”或“不一致”).

【问题提出】车轮为什么要做成圆形, 这里面有什么数学原理?
【合作探究】

探究 组:如图1,圆形车轮半径为
,其车轮轴心
到地面的距离始终为
.
探究 组:如图2,正方形车轮的轴心为
,若正方形的边长为
,求车轮轴心
最高点与最低点的高度差.
探究 组:如图3, 有一个破损的圆形车轮, 半径为
,破损部分是一个弓形,其所对圆心角为
,其车轮轴心为
,让车轮在地上无滑动地滚动一周,求点
经过的路程.
探究发现:车辆的平稳关键看车轮轴心是否稳定.
【拓展延伸】如图4,分别以正三角形的三个顶点 为圆心,以正三角形的边长为半径作
圆弧,这个曲线图形叫做“莱洛三角形”.
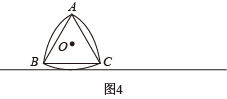

延伸发现:“莱洛三角形”在滚动时始终位于一组平行线之间,因此放在其上的物体也能够保持平衡,但其车轴中心 并不稳定.

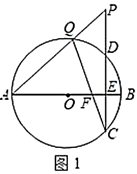

①求证: ;
②求y与x之间的函数关系式.
①如图3,用含有 的代数式表示
的周长;
②如图4, 恰好经过圆心
,求
内切圆半径与外接圆半径的比值.



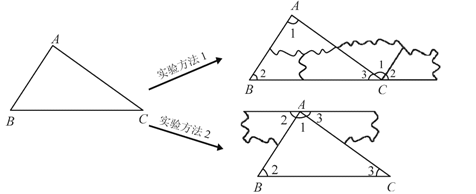
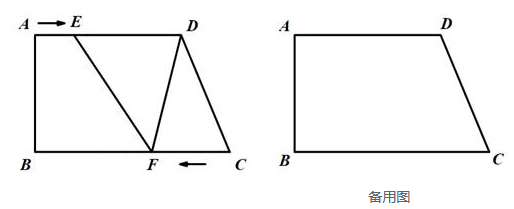
受到实验方法1的启发,小明形成了证明该结论的想法:实验1的拼接方法直观上看,是把和
移动到
的右侧,且使这三个角的顶点重合,如果把这种拼接方法抽象为几何图形,那么利用平行线的性质就可以解决问题了.
小明的证明过程如下:
已知:如图, . 求证:
.

证明:延长 , 过点
作
.
∴ ▲ (两直线平行,内错角相等),
( ▲ ).
∵(平角定义),
∴ .
