


例如:函数l的解析式为y=x2﹣1,当m=1时,它的相关函数l′的解析式为y=﹣x2+3(x<1).
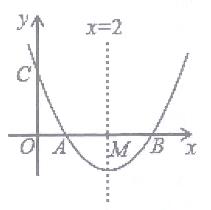
①已知点A、B的坐标分别为(0,2)、(6,2),图象F与线段AB只有一个公共点时,结合函数图象,求m的取值范围;
②若点C(x,n)是图象F上任意一点,当m﹣2≤x≤5时,n的最小值始终保持不变,求m的取值范围(直接写出结果).


日销售量y(千克)与时间第t(天)之间的函数关系如右图所示:

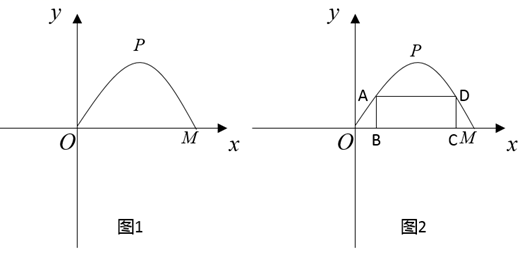
①抛物线型;②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.


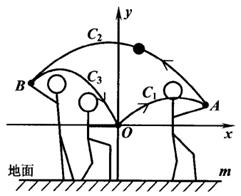
①当x的值为 ▲ 时,两小球到地面的距离相等;
②当x为何值时,两小球到地面的距离之差最大?最大是多少?
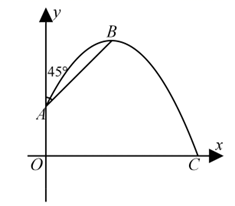

⑴
|
|
⑵
⑶
|
x/cm |
0 |
1 |
2 |
3 |
3.5 |
|
y1/cm |
2 |
3 |
3.8 |
4.4 |
4 |
|
y2/cm |
3.5 |
3.3 |
2.8 |
1.7 |
0 |