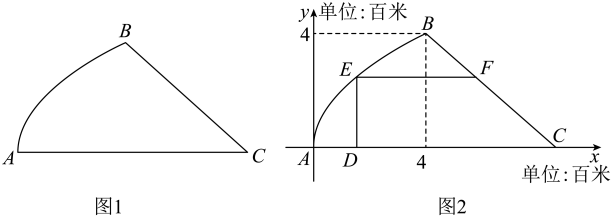
参考数据:;参考时间轴:

安全出口编号 |
|
|
|
|
疏散乘客用时(秒) | 120 | 140 | 190 | 160 |
则疏散乘客最快的一个安全出口的编号为.
①当时,若某家庭某月产生
生活垃圾,该家庭该月积分卡能兑换元;
②为了保证每个家庭每月积分卡兑换的金额均不超过当月垃圾分类投放带来的收益的%,则
的最大值为.
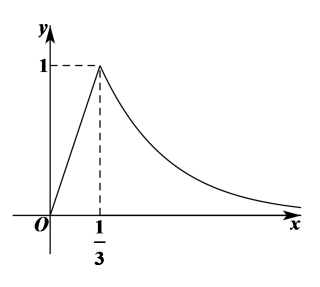
⑴若购买农资不超过2000元,则不给予优惠;
⑵若购买农资超过2000元但不超过5000元,则按原价给予9折优惠;
⑶若购买农资超过5000元,不超过5000元的部分按原价给予9折优惠,超过5000元的部分按原价给予7折优惠.
该县家境较困难的一户农民预购买一批农资,有如下两种方案:
方案一:分两次付款购买,实际付款分别为3150元和4850元;
方案二:一次性付款购买.
若采取方案二购买这批农资,则比方案一节省元.
年份 | 卫生总费用(亿元) | 个人现金卫生支出 | 社会卫生支出 | 政府卫生支出 | |||
绝对数(亿元) | 占卫生总费用比重 | 绝对数(亿元) | 占卫生总费用比重 | 绝对数(亿元) | 占卫生总费用比重 | ||
2012 | 28119.00 | 9656.32 | 34.34 | 10030.70 | 35.67 | 8431.98 | 29.99 |
2013 | 31668.95 | 10729.34 | 33.88 | 11393.79 | 35.98 | 9545.81 | 30.14 |
2014 | 35312.40 | 11295.41 | 31.99 | 13437.75 | 38.05 | 10579.23 | 29.96 |
2015 | 40974.64 | 11992.65 | 29.27 | 16506.71 | 40.29 | 12475.28 | 30.45 |
(数据来源于国家统计年鉴)
车型 | A | B | C | D | E | F |
价格 | 9万元 | 12万元 | 18万元 | 24万元 | 30万元 | 40万元 |
占比 | 5% | 15% | 25% | 35% | 15% | 5% |
全款购车:购车时一次性付款可优惠车价的3%;
分期付款:无价格优惠,购车时先付车价的一半,余下的每半年付一次,分4次付完,每次付车价的 .
①某位顾客现有a万元现金,欲购买价值a万元的某款车,付款后剩余的资金全部用于购买半年期的理财产品(该理财产品半年期到期收益率为1.8%),到期后,可用资金(含理财收益)继续购买半年期的理财产品,问:顾客选择哪一种付款方式收益更多?(计算结果精确到0.0001)
②为了激励购买理财产品,银行对采用分期付款方式的顾客,赠送价值1888元的大礼包,试问:这一措施对哪些车型有效?(计算结果精确到0.0001)
下表是该地近6年年底的新能源汽车的保有量(万辆)的统计数据:
年份 | 2018 | 2019 | 2020 | 2021 | 2022 |
t | 0 | 1 | 2 | 3 | 4 |
保有量 | 9.6 | 12.9 | 17.1 | 23.2 | 31.4 |
假设该地新能源汽车饱和量万辆.
附:线性回归方程中回归系数计算公式如下:
.
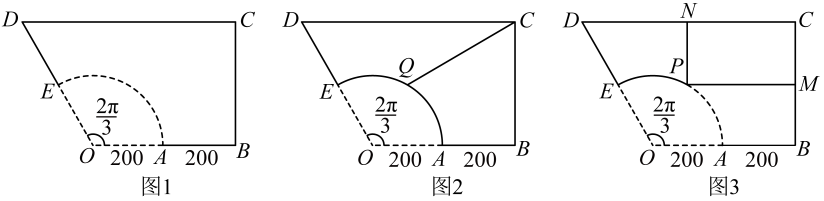
为了简单起见,现作如下假设:
假设1:绿地是由线段 ,
,
,
和弧
围成的,其中
是以
点为圆心,圆心角为
的扇形的弧,见图1;
假设2:线段 ,
,
,
所在的路行人是可通行的,圆弧
暂时未修路;
假设3:路的宽度在这里暂时不考虑;
假设4:路用线段或圆弧表示,休息亭用点表示.
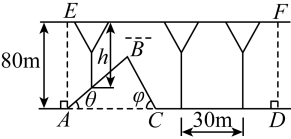
图1-图3中的相关边、角满足以下条件:
直线与
的交点是
,
,
.
米.
小区物业根据居民需求,决定在绿地修建一个休息亭.根据不同的设计方案解决相应问题,结果精确到米.
一般 | 良好 | 合计 | |
男 | 20 | 100 | 120 |
女 | 30 | 50 | 80 |
合计 | 50 | 150 | 200 |
附表及公式:
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中 ,
.
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 0.5 | 1 | 1.5 | 3 | 6 | 12 |
-0.7 | 0 | 0.4 | 1.1 | 1.8 | 2.5 |
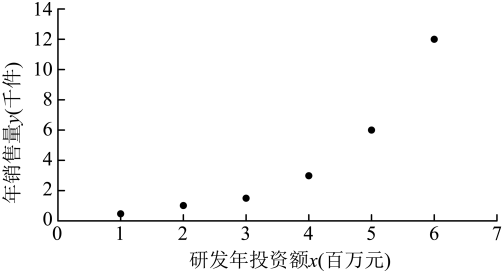
参考公式及数据: ,
,
,
,
.
经验回归方程 残差平方和 | ||
18.29 | 0.65 |
天数x | 1 | 2 | 3 | 4 | 5 | 6 |
抗体含量水平y | 5 | 10 | 26 | 50 | 96 | 195 |
根据以上数据,绘制了散点图.
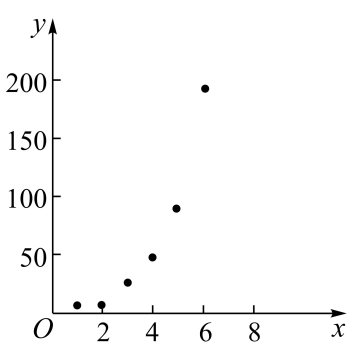
参考数据:其中 .
3.50 | 63.67 | 3.49 | 17.50 | 9.49 | 12.95 | 519.01 | 4023.87 |
参考公式:; ,
.