A款盲盒套餐 | B款盲盒套餐 | 合计 | |
年龄低于30岁 | 18 | 30 | 48 |
年龄不低于30岁 | 22 | 10 | 32 |
合计 | 40 | 40 | 80 |
附: , 其中
,
P( | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
2.706 | 3.841 | 5.024 | 6.635 | 0.828 |
附:
大气湿度x | 45% | 59% | 66% | 68% | 69% | 70% | 72% | 77% | 80% | 88% |
空壳率y | 18% | 21% | 25% | 27% | 26% | 29% | 31% | 32% | 33% | 37% |
附:经验回归方程系数: ,
,
,
,
,
.
超市 | A | B | C | D | E | F | G |
广告支出 | 1 | 2 | 4 | 6 | 10 | 13 | 20 |
销售额 | 19 | 32 | 44 | 40 | 52 | 53 | 54 |
附注:参考数据 , 回归方程
中斜率和截距的最小二乘估计公式分别为:
.
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
提案数量y(单位:千件) | 5.762 | 6.069 | 5.641 | 5.875 | 5.857 | 5.769 | 5.21 | 5.36 | 5.488 | 5.044 |
参考公式:相关系数 ,
.
参考数据: .

附: ,
,
超过M | 不超过M | |
上班时间 | ||
下班时间 |

附: .
0.100 | 0.050 | 0.010 | 0.001 | |
k | 2.706 | 3.841 | 6.635 | 10.828 |
①求随机变量的分布列;
②证明:单调递增,且小于3.
电解电容为次品 | 电解电容为正品 | |
铝箔为次品 | 174 | 76 |
铝箔为正品 | 108 | 142 |
每天的浏览量 | ||
每天的购买量 | 300 | 900 |
天数 | 36 | 24 |
以每天的浏览量位于各区间的频率代替浏览量位于该区间的概率.
参考公式及数据: , 其中,
习惯固定在左侧接听电话 | 习惯固定在右侧接听电话 | 总计 | |
脑瘤部位在左侧的病人 | a | b | 42 |
脑瘤部位在右侧的病人 | c | d | 46 |
总计 | a+c | b+d | 88 |
一般 | 激动 | 总计 | |
男性 | 90 | 120 | |
女性 | 25 | ||
总计 | 200 |
附: , 其中
.
0.100 | 0.050 | 0.010 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
投入额 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
年收入的附加额 | 3.6 | 4.1 | 4.8 | 5.4 | 6.2 | 7.5 | 7.9 | 9.1 |
【参考数据】 ,
,
.
【附】在经验回归方程中,
,
.
一般 | 良好 | 合计 | |
男 | 20 | 100 | 120 |
女 | 30 | 50 | 80 |
合计 | 50 | 150 | 200 |
附表及公式:
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中 ,
.
现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.
假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为 , 且每局赌赢可以赢得1元,每一局赌徒赌输的概率为
, 且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为
, 赌博过程如下图的数轴所示.

当赌徒手中有n元( ,
)时,最终输光的概率为
, 请回答下列问题:

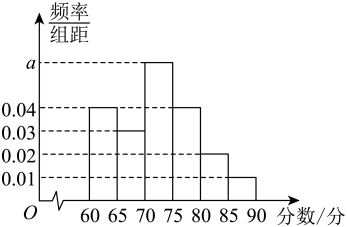
竞赛成绩(单位:分) | |||||||
人数(单位:人) | 6 | 14 | 30 | 74 | 42 | 23 | 11 |

附: , 其中
.
0.10 | 0.05 | 0.01 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
优秀 | 不够优秀 | 总计 | |
“物化生”组合 | 40 | ||
“物化地”组合 | |||
总计 |
第一步:将原始成绩从高到低排列,按人数比例划分为20个赋分区间.
第二步:对每个区间的原始成绩进行等比例转换,公式为:
其中分别是该区间原始成绩的最低分、最高分;
分别是该区间等级分的最低分、最高分;
为某考生原始成绩,
为转换结果.
第三步:将转换结果四舍五入,确定为该考生的最终等级分.
本次联考采用浙江选考等级赋分制,已知全市所有的考生原始成绩从高到低前(最低分为80分)的考生被划分至
的赋分区间,甲、乙两位考生的化学原始成绩分别为
, 最终的等级分为98、99.试问:本次联考全市化学原始成绩的最高分是否可能是91分?请说明理由.
月份 | ||||||
广告投入量 | ||||||
收益 |
他们分别用两种模型① , ②
分别进行拟合,得到相应的回归方程并进行残差分析,得到如下图所示的残差图及一些统计量的值.
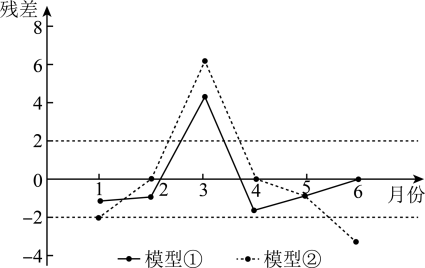
附:回归方程中斜率和截距的最小二乘估计公式分别为:
,
.
(i)剔除异常数据后求出(1)中所选模型的回归方程;
(ii)若广告投入量 , 求该模型收益的预报值是多少?

喜欢足球 | 不喜欢足球 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 |
附:
0.1 | 0.05 | 0.01 | 0.005 | 0.001 | |
2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
球队输球 | 球队赢球 | 总计 | |
甲参加 | 2 | 30 | 32 |
甲未参加 | 8 | 10 | 18 |
总计 | 10 | 40 | 50 |
附: .
参考数据:
a | 0.05 | 0.01 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |
①证明:;
②利用球员甲数据统计,给出 ,
的估计值,并求出R的估计值.



身高/ | ||||||
体重/ |

根据表中数据计算得到关于
的线性回归方程对应的直线的斜率为
.
①估计体重超过的频率
,
②视频率为概率,从该地区大量高中男生中随机选出人,记这
人中体重超过
的人数为
, 求
的分布列及其数学期望(用(1)中的回归方程估测这
位男生的体重).

体育迷 | 非体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:
0.050 | 0.010 | 0.001 | |
3.841 | 6.635 | 10.828 |

名女生成绩频数分布表:
成绩 | ||||
频数 | 10 | 10 | 6 | 4 |
附:
0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 | |
2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
男生 | 女生 | 合计 | |
防疫标兵 | |||
非防疫标兵 | |||
合计 |

参考数据:独立性检验临界值表
使用直播销售情况与年龄列联表
年轻人 | 非年轻人 | 合计 | |
经常使用直播售用户 | |||
不常使用直播销售用户 | |||
合计 |

附:若随机变量X服从正态分布 , 则:
,
,
.