 B .
B . 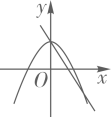 C .
C .  D .
D . 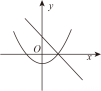
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 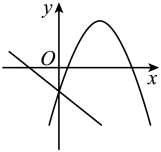
 B .
B .  C .
C .  D .
D . 

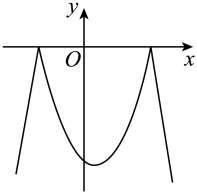

x | 1.0 | 1.1 | 1.2 | 1.3 |
x2+12x | 13 | 14.41 | 15.84 | 17.29 |
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
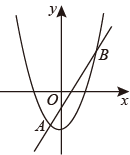
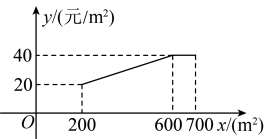

|
甲 |
乙 |
丙 |
|
|
单价(元/棵) |
14 |
16 |
28 |
|
合理用地(m2/棵) |
0.4 |
1 |
0.4 |





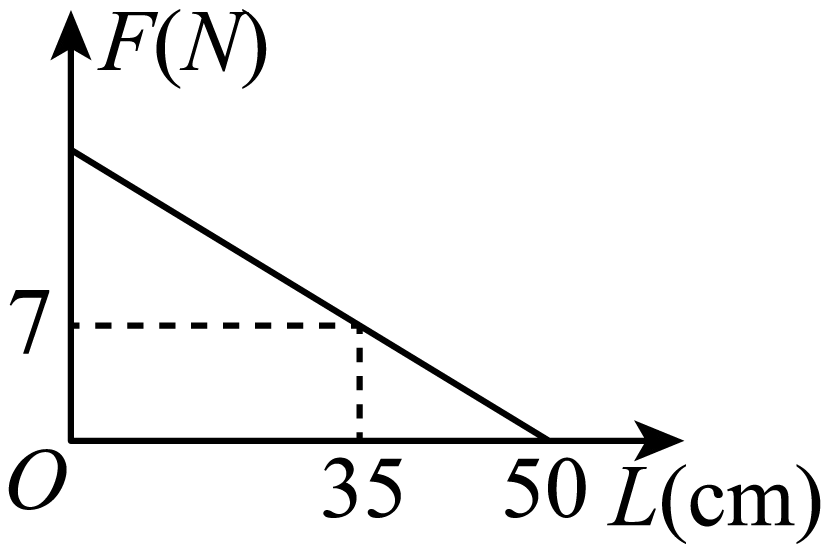 B .
B . 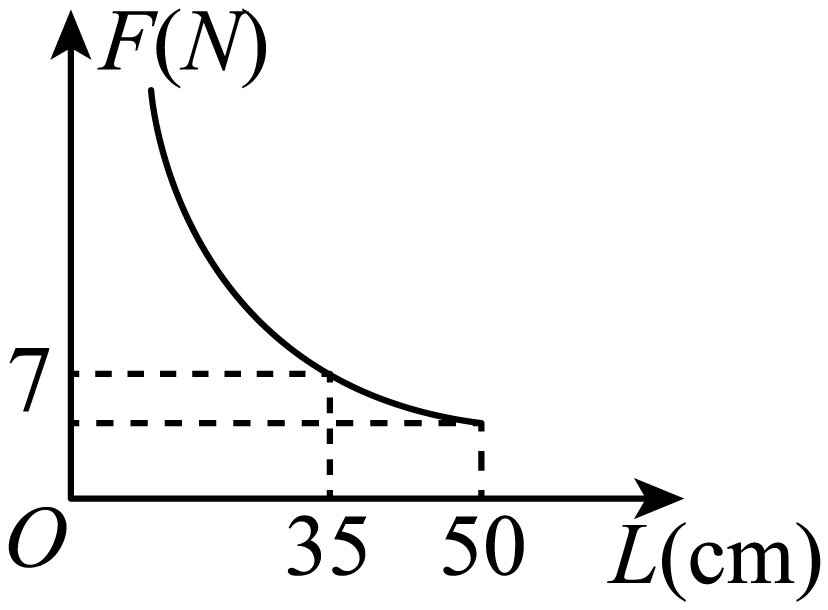 C .
C . 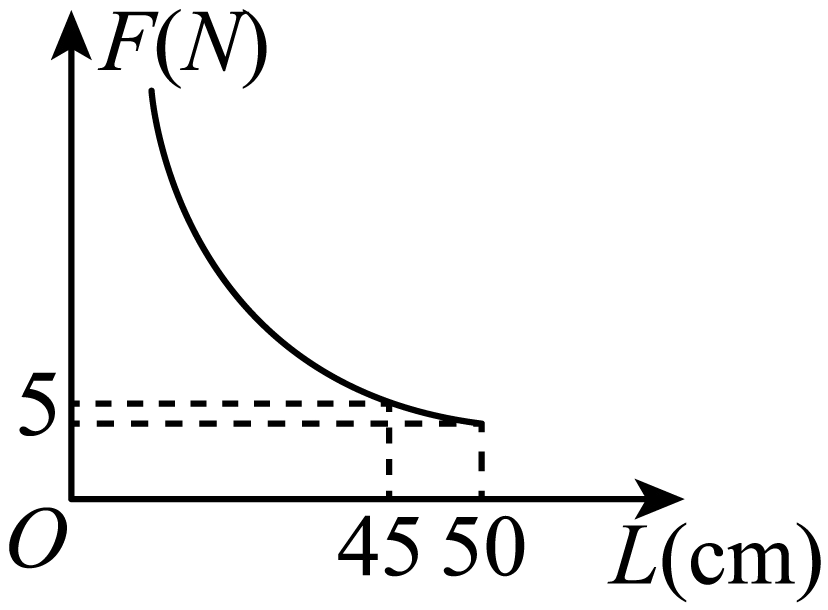 D .
D . 
 B .
B .  C .
C .  D .
D . 
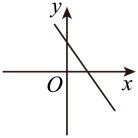 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 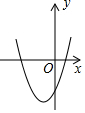

|
托盘 |
30 |
25 |
20 |
15 |
10 |
|
容器与水的总质量 |
10 |
12 |
15 |
20 |
30 |
|
加入的水的质量 |
5 |
7 |
10 |
15 |
25 |
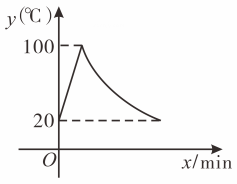
把上表中的与
各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的
关于
的函数图象.

①猜测与
之间的函数关系,并求
关于
的函数表达式;
②求关于
的函数表达式;
③当时,
随
的增大而(填“增大”或“减小”),
随
的增大而(填“增大”或“减小”),
的图象可以由
的图象向(以“上”或“下”或“左”或“右”)平移得到.