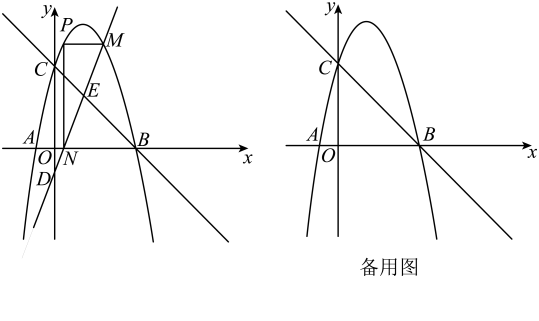

②根据d的不同取值,试探索点P的个数情况.


①当t为何值时,四边形PEDF是平行四边形;
②设△BCF的面积为S,当t为何值时,S最大?最大值是多少?
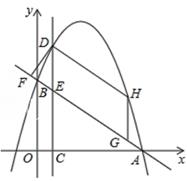
①当时,求证:PC=CD;
②当a≠1时,请用合适的式子表示(直接写结果).
|
x |
… |
|
0 |
1 |
2 |
3 |
… |
|
y |
… |
0 |
3 |
4 |
3 |
0 |
… |
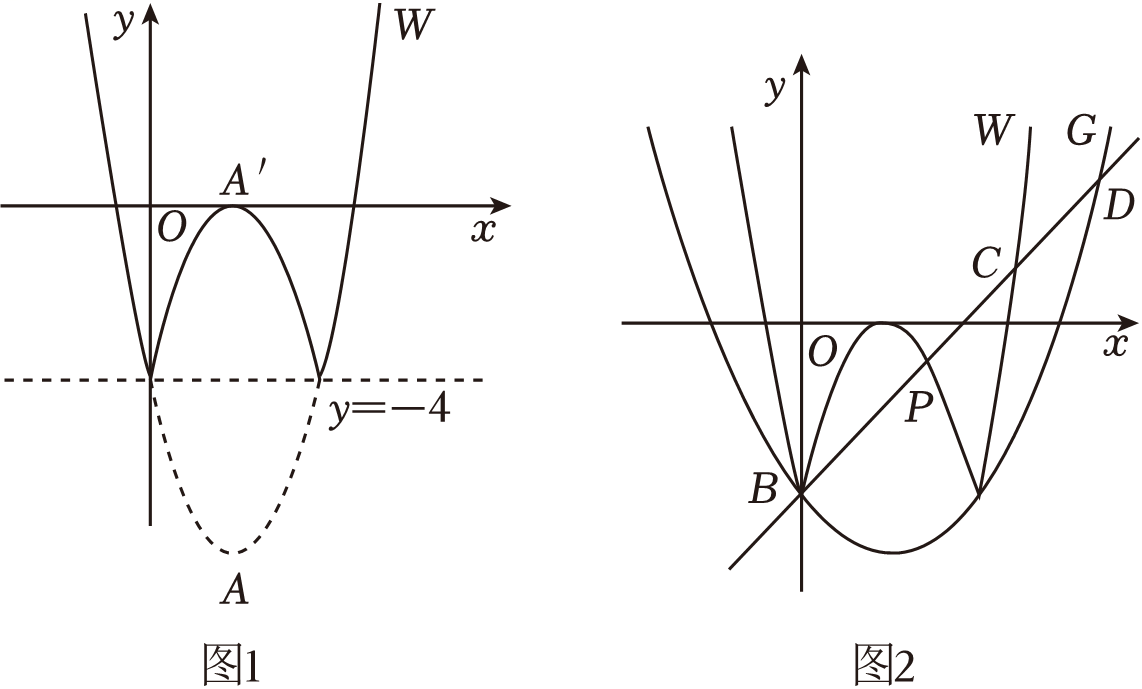
①如图2,若直线过点M , 交x轴于点D , 在x轴上取点
, 连接EM , 求∠DME的度数.
②把抛物线在x轴下方图象沿x轴翻折得到新图象(如图3).当直线
与新图象有两个公共点时,请直接写出n的取值范围.

①抛物线C'的解析式为 ▲(用含m的关系式表示);
②求m的取值范围;
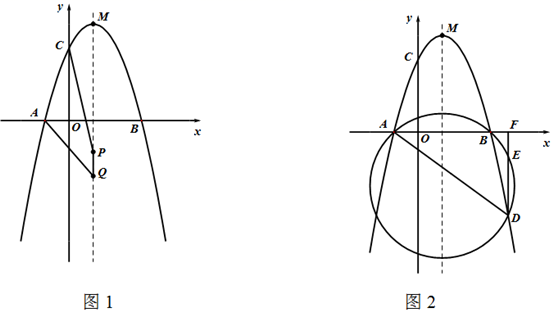
①求点的坐标;
②设射线与
相交于点
, 交
于点
, 将
绕点
旋转一周,旋转后的三角形记为
, 求
的最小值.