备考2024年中考数学探究性训练专题23 图形的旋转

更新时间：2024-04-01 浏览次数：38 类型：二轮复习

一、选择题

1. (2023·南湖模拟) 如图，正方形 $\text{[math]}$ 边长为4，点E在边 $\text{[math]}$ 上运动，在 $\text{[math]}$ 的左侧作等腰直角三角形 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ .喜欢探究的小亮通过独立思考，得到以下两个结论：①当点E与点D重合时， $\text{[math]}$ ；②当线段 $\text{[math]}$ 最短时， $\text{[math]}$ .下列判断正确的是（）

A . ①，②都正确 B . ①，②都错误 C . ①正确，②错误 D . ①错误，②正确

答案解析收藏纠错 + 选题

二、填空题

2. (2019·江北模拟) 一副三角板如图所示，叠放在一起.若固定△AOB，将△ACD绕着公共点A按顺时针方向旋转α度(0＜α＜180).请你探索，当△ACD的一边与△AOB的一边平行时，相应的旋转角α的度数.

答案解析收藏纠错 + 选题
3. (2021·安徽模拟) 如图，Rt△BAC ， ∠ACB=30°，∠BAC=90°，将Rt△BAC绕点A旋转一定度数，点C与点C'重合，点B与点B'重合，当C、B、C'三点在同一条直线时，请完成下列探究：
1. （1）这个旋转角=°；
2. （2）此时， $\text{[math]}$ ．
答案解析收藏纠错 + 选题
4. (2021·甘肃模拟) 如图， $\text{[math]}$ 是正方形 $\text{[math]}$ 内点，且 $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转得到 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，请完成下列探究：
1. （1） $\text{[math]}$ 的度数为 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为.
答案解析收藏纠错 + 选题
5. (2022·安徽模拟) 四边形ABCD是矩形，以点D为旋转中心，顺时针旋转矩形ABCD，得到矩形DEFG， $\text{[math]}$ ， $\text{[math]}$ ，试探究：
1. （1）如图1，当点E落在BC上时，CE的长度为；
2. （2）如图2，O是对角线BD的中点，连接EO，FO，设 $\text{[math]}$ 的面积为s，在矩形DEFG的旋转过程中，s的取值范围为．
答案解析收藏纠错 + 选题
6. (2019九上·衢州期中) 如图，在平面直角坐标系xOy中，已知抛物线 y=-x(x-3)(0≤x≤3) 在x轴上方部分记作C₁ ，它与x轴交于点O，A₁ ，将C₁绕点A₁旋转180°得C₂ ， C₂与x 轴交于另一点A₂ ．继续操作并探究：将C₂绕点A₂旋转180°得C₃ ，与x 轴交于另一点A₃；将C₃绕点A ₂旋转180°得C₄ ，与x 轴交于另一点A₄ ，这样依次得到x轴上的点A₁ ， A₂ ， A₃ ， …，A_n ， …，及抛物线C₁ ， C₂ ， …，C_n ， …．则点A₄的坐标为；C_n的顶点坐标为(n为正整数，用含n的代数式表示) ．

答案解析收藏纠错 + 选题

三、理论探究题

7. (2023九上·鸡西月考) 问题情境：数学课上，老师引导同学们以“正方形中线段的旋转”为主题开展数学活动．已知正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点E是射线 $\text{[math]}$ 上一点（不与点C重合），连接 $\text{[math]}$ ，将 $\text{[math]}$ 绕点E顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）特例分析：如图1，当点E与点D重合时，则 $\text{[math]}$ =；
2. （2）深入谈及：当点E不与点D重合时，（1）中的结论是否仍然成立？若成立，请在图2与图3中选择一种情况进行证明；若不成立，请说明理由；
答案解析收藏纠错 + 选题
8. (2023九上·丰满期中)
1. （1）【模型感知】如图①，在正方形ABCD中，点E是对角线AC上一点（不与点A、C重合），连接BE ，将线段BE绕点B逆时针旋转90°得到线段BE'，连接AE^' ，求证：AE'＝CE；
2. （2）【模型发展】如图②，在正方形ABCD中，点E是对角线CA的延长线上的一点，连接BE ，将线段BE绕点B逆时针旋转90°得到线段BE'，连接AE'，线段AE^'与CE的数量关系为，AE'与CE所在直线的位置关系为（不需证明）；
3. （3）【解决问题】如图③，在正方形ABCD中，点E是对角线AC延长线上的一点，连接BE ，将线段BE绕点B逆时针旋转90°，得到线段BE'，连接AE'，EE'，若AC＝3CE ，则 $\text{[math]}$ ＝．
答案解析收藏纠错 + 选题
9. (2023九上·江源月考) 如图①．四边形ABCD与四边形AEFG是共一个顶点的两个大小不同的正方形．
1. （1）操作发现：如图②．正方形AEFG绕顶点A逆时针旋转，使点E落在边AD上时．填空：
  ①线段BE与IG的数量关系是
  ②∠ABE与∠ADG的关系是
2. （2）猜想与证明：如图③，正方形AEFG绕顶点A逆时针旋转某一角度α（0<α< 90°）时．猜想（1）中的结论是否成立？并证明你的结论：
3. （3）拓展应用：如图④．正方形AEFG绕顶点A逆时针旋转，使点F落在边AD上时，若AB= $\text{[math]}$ ． AF=1，则BE=
答案解析收藏纠错 + 选题
10. (2023九上·天河期中) 如图，在正方形 $\text{[math]}$ 中，E、F分别是边 $\text{[math]}$ 、 $\text{[math]}$ 上的两点，且 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别交正方形的对角线 $\text{[math]}$ 于G、H两点，将 $\text{[math]}$ 绕点A顺时针旋转90°后，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 平分 $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ ；
3. （3）试试探索 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三条线段间的数量关系，并加以证明．
答案解析收藏纠错 + 选题
11. (2023九上·深圳月考) 通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．
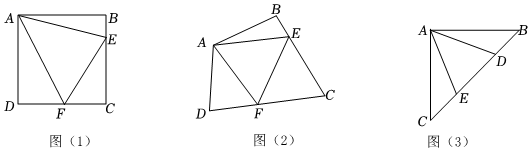
原题：如图1，点E ， F分别在正方形ABCD的边BC ， CD上，∠EAF＝45°，连接EF ，则EF＝BE＋DF ，试说明理由．
1. （1）思路梳理
  ∵AB＝CD ， ∴把△ABE绕点A逆时针旋转90°至△ADG ，可使AB与AD重合．∵∠ADC＝∠B＝90°∠FDG＝180°，∴点F ， D ， G共线．根据（从“SSS ， ASA ， AAS ， SAS”中选择填写），易证△AFG≌，得EF＝BE＋DF ．
2. （2）类比引申
  如图2，四边形ABCD中，AB＝AD ， ∠BAD＝90°，点E ， F分别在边BC ， CD上，∠EAF＝45°．若∠B ， ∠D都不是直角，则当∠B与∠D满足等量关系时，仍有EF＝BE＋DF ．
3. （3）联想拓展
  如图3，在△ABC中，∠BAC＝90°，AB＝AC ，点D ， E均在边BC上，且∠DAE＝45°．猜想BD ， DE ， EC应满足的等量关系，并写出推理过程．
4. （4）思维深化
  如图4，在△ABC中，∠BAC＝60°，AB＝AC ，点D ， E均在直线BC上，点D在点E的左边，且∠DAE＝30°，当AB＝4，BD＝1时，直接写出CE的长．
答案解析收藏纠错 + 选题
12. (2024·从江模拟) 【问题情境】
如图 $\text{[math]}$ ，点 $\text{[math]}$ 为正方形 $\text{[math]}$ 内一点， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 按顺时针方向旋转 $\text{[math]}$ ，得到 $\text{[math]}$ 点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ 延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）四边形 $\text{[math]}$ 的形状是；
2. （2） $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ，则正方形 $\text{[math]}$ 的面积为；
3. （3） $\text{[math]}$ 如图 $\text{[math]}$ ，若 $\text{[math]}$ ，请猜想线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系并加以证明．
答案解析收藏纠错 + 选题
13. (2023九上·安吉月考) 如图1，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E分别是AC、BC的中点，连接DE ．
1. （1）探索发现：
  图1中， $\text{[math]}$ 的值为， $\text{[math]}$ 的值为．
2. （2）拓展探究
  若将△CDE绕点C旋转，在旋转过程中 $\text{[math]}$ 的大小有无变化？请仅就图2的情形给出证明．
3. （3）问题解决
  当△CDE旋转至A ， D ， C三点共线时，直接写出线段BE的长．
答案解析收藏纠错 + 选题
14. (2024九上·从江月考) 【发现证明】如图(1)所示，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，在判断BE，EF，FD之间的数量关系时，小聪把△ABE绕点A逆时针旋转90°至△ADG，通过证明△AEF≌△AGF；从而发现并证明了EF=BE+FD.
1. （1）【类比引申】
  如图(2)所示，点E，F分别在正方形ABCD的边CB，CD的延长线上，∠EAF=45°，连接EF，请根据小聪的发现给你的启示写出EF，BE，DF之间的数量关系，并证明；
2. （2）【联想拓展】
  如图(3)所示，∠BAC=90°，AB=AC，点E，F在边BC上，且∠EAF=45°，若BE=3，EF=5，求CF的长.
答案解析收藏纠错 + 选题
15. (2024九上·苍溪期末) 把两个等腰直角三角形 $\text{[math]}$ 和 $\text{[math]}$ 按图①所示的位置摆放，将 $\text{[math]}$ 绕点C逆时针旋转 $\text{[math]}$ （ $\text{[math]}$ ）到图②所示位置，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）特例问题：如图①， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是， $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是；
2. （2）探索解决：如图②，（1）中 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系和位置关系是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
3. （3）拓展应用：如图③，点D在 $\text{[math]}$ 内部，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
16. (2024九上·伊通期末) 已知 $\text{[math]}$ 是等腰三角形， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转得到 $\text{[math]}$ ，点 $\text{[math]}$ 、点 $\text{[math]}$ 的对应点分别是点 $\text{[math]}$ 、点 $\text{[math]}$ ．
1. （1）感知：如图①，当 $\text{[math]}$ 落在 $\text{[math]}$ 边上时， $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是：(不需要证明)；
2. （2）探究：如图②，当 $\text{[math]}$ 落在 $\text{[math]}$ 的左侧时， $\text{[math]}$ 与 $\text{[math]}$ 是否相等？如果相等，请证明；如果不相等，请说明理由；
3. （3）应用：如图③，若 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ，则 $\text{[math]}$ 度．
答案解析收藏纠错 + 选题
17. (2024九上·长春期末) 【教材呈现】如图是华师版九年级上册数学教材第 $\text{[math]}$ 页的部分内容．
如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 与 $\text{[math]}$ 的中点，根据画出的图形，可以猜想： $\text{[math]}$ ，且 $\text{[math]}$ ．
对此，我们可以用演绎推理给出证明 $\text{[math]}$ 无需证明 $\text{[math]}$
1. （1）【感知】如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 和 $\text{[math]}$ 的中点，求 $\text{[math]}$ 的长；
2. （2）【应用】如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转一定的角度 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ；
3. （3）【拓展】如图 $\text{[math]}$ ，在等边 $\text{[math]}$ 中， $\text{[math]}$ 是射线 $\text{[math]}$ 上一动点 $\text{[math]}$ 点 $\text{[math]}$ 在点 $\text{[math]}$ 右侧 $\text{[math]}$ ，连接 $\text{[math]}$ ，把线段 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 中点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024九上·宁江期末)
1. （1）【性质探究】如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， AB＝AC ，点D在斜边BC上，将△ABD绕点A逆时针旋转90°得到△ACE．
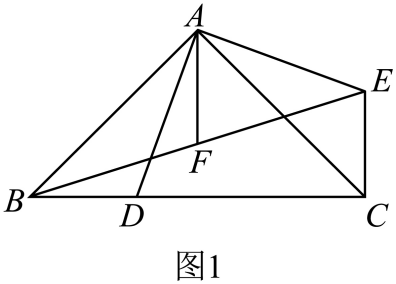
  ①直线BD与CE的位置关系为；
  ②若点F为BE的中点，连接AF ，请探究线段AF与CD的数量关系，并给予证明．
2. （2）【拓展应用】
  如图2，已知点E是正方形ABCD的边BC上任意一点，以AE为边作正方形AEFG ，连接BG，点H为BG的中点，连接AH ．若AB＝4，BE＝3，求AH的长．
答案解析收藏纠错 + 选题
19. (2023九上·丰城月考) 综合与实践
如图1，已知点G在正方形ABCD的对角线AC 上，GE⊥BC ，垂足为E ， GF⊥CD ，垂足为F ．
1. （1）【证明与推断】
  ①四边形CEGF的形状是 ▲；
  ② $\text{[math]}$ 的值为 ▲；
2. （2）【探究与证明】
  在图1的基础上，将正方形CEGF绕点C按顺时针方向旋转α角（0°<α<45°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；
3. （3）【拓展与运用】
  如图3，在（2）的条件下，正方形CEGF 在旋转过程中，当B、E、F三点共线时，探究AG和GE的位置关系，并说明理由．
答案解析收藏纠错 + 选题
20. (2023九上·金沙期中) 综合与实践：
1. （1）问题情景：如图1，已知等边 $\text{[math]}$ 和它内部一点D，把线段BD绕点B逆时针旋转 $\text{[math]}$ 得到线段BE，连接DE，CE，射线AD，CE交于点F，则AD与CE数量关系是， $\text{[math]}$ .（填空）
2. （2）类比探究：如图2，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D是AC边上一点，过点D作 $\text{[math]}$ 交AB于点E，将 $\text{[math]}$ 绕点A旋转得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，在旋转的过程中，设直线 $\text{[math]}$ ， $\text{[math]}$ 交于点F，探索 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系和 $\text{[math]}$ 的度数；
3. （3）拓展应用：如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，以AB为斜边作等腰直角三角形ABD，若 $\text{[math]}$ ，求线段的AB长（直接写出答案）.
答案解析收藏纠错 + 选题
21. (2023九上·肇州月考)
1. （1）问题提出
  如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ，点M为 $\text{[math]}$ 内一点，将线段 $\text{[math]}$ 绕点A按逆时针方向旋转 $\text{[math]}$ 的度数得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为．
2. （2）问题解决
  如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，过B点的射线 $\text{[math]}$ 交 $\text{[math]}$ 边于点D ，且 $\text{[math]}$ ， M为射线 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，当 $\text{[math]}$ 为直角三角形时，求 $\text{[math]}$ 的长．
3. （3）拓展探究
  如图3，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， E为直线 $\text{[math]}$ 上动点，将 $\text{[math]}$ 绕D逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．（直接写出结果）
答案解析收藏纠错 + 选题
22. (2023九上·大同期中) 综合与实践
问题情境：如图1，正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ 有公共顶点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，现将正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 按顺时针方向旋转，旋转角为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

图1图2图3
1. （1）猜想证明：猜想图2中 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系并证明；
2. （2）探究发现：如图3，当 $\text{[math]}$ 时，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ 垂直平分 $\text{[math]}$ ；
3. （3）拓展延伸：在旋转过程中，当 $\text{[math]}$ 的面积最大时，直接写出此时旋转角 $\text{[math]}$ 的度数和 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
23. (2023九上·抚松月考) 已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠MAN的两边分别与射线CB、DC相交于点E、F，且∠MAN = 60*．
1. （1） [初步感知]
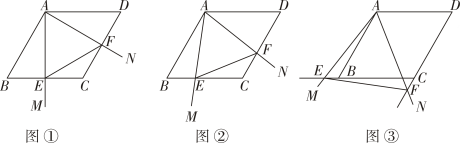
  当E是线段CB的中点时（如图①），AE与EF的数量关系为
2. （2） [深入探究]
  如图②，将图①中的∠MAN绕点A顺时针旋转α（0°<α< 30°），（1）中的结论还成立吗？说明理由；
3. （3） [拓展应用]
  如图③，将图①中∠MAN绕点A继续顺时针旋转，当α= 45°时，直接写出EB的长．
答案解析收藏纠错 + 选题
24. (2023九上·仙居期中)
1. （1）特殊情景：如图 $\text{[math]}$ ，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为顶点作一个角，角的两边分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，探究：线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并说明理由．
2. （2）类比猜想：类比特殊情景，在上述 $\text{[math]}$ 条件下，把“ $\text{[math]}$ ”改成一般情况“ $\text{[math]}$ ， ”如图 $\text{[math]}$ ，小明猜想：线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系是否仍然成立？若成立，请你写出结论；若不成立，请写出理由．
3. （3）解决问题：如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 均在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，若 $\text{[math]}$ ，计算 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
25. (2023九上·吉州月考) 问题解决
一节数学课上，老师提出了这样一个问题：如图①，点P是等边 $\text{[math]}$ 内的一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .你能求出 $\text{[math]}$ 的度数和等边 $\text{[math]}$ 的面积吗?小明通过观察、分析、思考，形成了如下思路：
如图①将 $\text{[math]}$ 绕点B逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，可得 $\text{[math]}$ 是等边三角形，根据勾股定理逆定理可得 $\text{[math]}$ 是直角三角形，从而使问题得到解决.
1. （1）结合小明的思路完成填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
2. （2）类比探究
  ①.如图②，若点P是正方形 $\text{[math]}$ 内一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数和正方形的面积.
  ②.如图③，若点P是正方形 $\text{[math]}$ 外一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数和正方形的面积.
答案解析收藏纠错 + 选题
26. (2023九上·长春月考) 如图(1)，已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．易证四边形CEGP是正方形．
1. （1）推断， $\text{[math]}$ 的值为；
2. （2）探究与证明：将正方形CEGP绕点C顺时针方向旋转α角(0°<α<45°)，如图(2)所示，试探究线段NG与BE之间的数量关系，并说明理由：
3. （3）拓展与运用：正方形CECF在旋转过程中，当B，E，P三点在一条直线上时，如图(3)所示，延长CG交AD于点H．若AG=6，GH= $\text{[math]}$ ．则BC=
答案解析收藏纠错 + 选题
27. (2023·贵州模拟) 综合与实践
1. （1）问题提出
  如图①，在 $\text{[math]}$ 与 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，连接 $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的形状是．
2. （2）问题探究
  如图②，将图①中的 $\text{[math]}$ 绕点 $\text{[math]}$ 按逆时针方向旋转，使点 $\text{[math]}$ 落在 $\text{[math]}$ 边上，试判断 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的数量关系，并说明理由；
3. （3）拓展延伸
  在图②中，若 $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 按逆时针方向旋转，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上时，求线段 $\text{[math]}$ 的长（用含 $\text{[math]}$ 的式子表示）．
答案解析收藏纠错 + 选题
28. (2023·铜仁模拟) 定义：在一个等腰三角形底边的高线上所有点中，到三角形三个顶点距离之和最小的点叫做这个等腰三角形的“近点”，“近点”到三个顶点距离之和叫做这个等腰三角形的“最近值”．
1. （1）【基础巩固】如图1，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的高，已知 $\text{[math]}$ 上一点E满足 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ；
2. （2）【尝试应用】如图2，等边 $\text{[math]}$ 边长为 $\text{[math]}$ ， E为高线 $\text{[math]}$ 上的点，将 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，请你在此基础上继续探究出等边 $\text{[math]}$ 的“最近值”；
3. （3）【拓展提高】如图3，在菱形 $\text{[math]}$ 中，过 $\text{[math]}$ 的中点E作 $\text{[math]}$ 垂线交 $\text{[math]}$ 的延长线于点F，连接 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ “最近值”的平方．
答案解析收藏纠错 + 选题

四、实践探究题

29. (2022·潍坊)
1. （1）【情境再现】
  甲、乙两个含 $\text{[math]}$ 角的直角三角尺如图①放置，甲的直角顶点放在乙斜边上的高的垂足O处，将甲绕点O顺时针旋转一个锐角到图②位置．小莹用作图软件Geogebra按图②作出示意图，并连接 $\text{[math]}$ ，如图③所示， $\text{[math]}$ 交 $\text{[math]}$ 于E， $\text{[math]}$ 交 $\text{[math]}$ 于F，通过证明 $\text{[math]}$ ，可得 $\text{[math]}$ ．
  请你证明： $\text{[math]}$ ．
2. （2）【迁移应用】
  延长 $\text{[math]}$ 分别交 $\text{[math]}$ 所在直线于点P，D，如图④，猜想并证明 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系．
3. （3）【拓展延伸】
  小亮将图②中的甲、乙换成含 $\text{[math]}$ 角的直角三角尺如图⑤，按图⑤作出示意图，并连接 $\text{[math]}$ ，如图⑥所示，其他条件不变，请你猜想并证明 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系．
答案解析收藏纠错 + 选题
30. (2023九上·潞州期中) 综合与实践
问题情境：
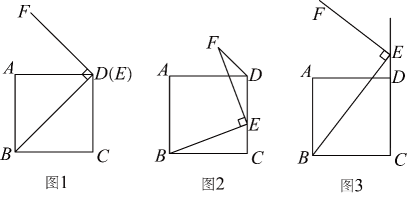
在“综合与实践”课上，老师提出如下问题：如图 $\text{[math]}$ ，在矩形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将矩形纸片沿对角线 $\text{[math]}$ 剪开，得到两个全等的直角三角形纸片 $\text{[math]}$ 和 $\text{[math]}$ ，将 $\text{[math]}$ 固定不动， $\text{[math]}$ 绕点 $\text{[math]}$ 按顺时针方向旋转一定角度，得到 $\text{[math]}$ ，其中点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ ．如图 $\text{[math]}$ ，当点 $\text{[math]}$ 落在 $\text{[math]}$ 边上时，连结 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
1. （1）数学思考：
  请你解答老师提出的问题．
2. （2）深入探究：
  老师将图2中的 $\text{[math]}$ 绕点C继续按顺时针方向旋转，在旋转的过程中，让同学们提出新的问题
  ①“善思小组”提出问题：如图3，当点 $\text{[math]}$ 落在 $\text{[math]}$ 的延长线上时，连结 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
  ②“智慧小组”提出问题：如图4，当点 $\text{[math]}$ 落在 $\text{[math]}$ 的延长线上时，连结 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题